Description
A Parabola is a Conic Section and describes the path (or trajectory) taken by a ball as it is thrown in the air.
An important characteristic of a parabola-shaped reflector is that any beam of light, sound or other energy which enters travelling parallel to its main axis is reflected through a single point called its focus. Conversely, light that originates from a point source at the focus is reflected into a parallel beam. This makes parabolic forms (i.e. parabloids) very useful for microphones and spotlight reflectors for example.
Parabolas can be drawn as the graph of y=x2 but there are other ways of drawing a parabola which exploit its various mathematical properties.
Constructions
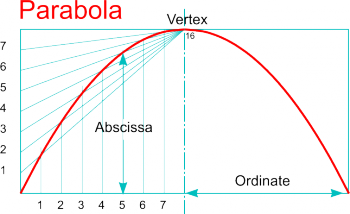
| Drawing a Parabola within a Rectangle
|
- A parabola may be drawn by first constructing a rectangle and dividing into 2 as shown.
- Divide half of the base and the height into the same number of equal parts.
- Number the divisions from outside the rectangle to the its centre on the base (i.e. left to right) and bottom to top on the side.
- Draw vertical lines through all the divisions along the base then radial lines from the top centre (which will become the Vertex) to each of the vertical divisions to intersect them - i.e. Point 1 is where vertical Line 1 is intersected by Radial line 1.
- Repeat the process for the right hand half of the parabola but note that the base divisions will now be numbered right to left.
- Sketch a fair curve through the points (or use French Curves or a flexible strip for example)
|
|
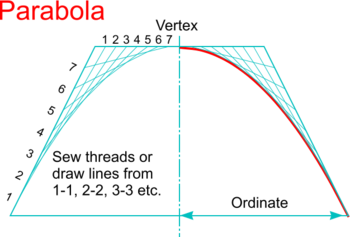
| Curve Stitching
|
- Curve Stitching (or String Art) is a craft technique used to create patterns from parabolas and other curves by sewing threads between points along two intersecting lines.
- The technique was invented by Mary Everest Boole at the end of the 19th Century to make maths more interesting to children and became very popular during the 1960's to decorate gift cards for example.
- Instead of sewing threads, lines can be drawn between the points and a parabola created by sketching a fair curve to touch the lines (or use French Curves or a flexible strip for example)
Note:
The idea of creating curves using straight lines is put to practical use to design and build curved roofs and curve-sided towers and even bridges using straight pieces of material - see Saddle Roofs and Cooling Towers or Hyperboloid structures and The Mathematical Bridge at Cambridge for examples.
|
|
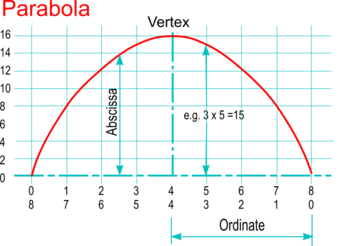
| Using measured Abscissae
|
- A property of the parabola is that the abscissa, that part of a diameter of a conic between its vertex and an ordinate, is ‘proportional to the product of the parts into which it divides the double ordinate’.
- Start by drawing a horizontal ordinate, say 4 units long, then doubling it to become a line 8 units long.
- Number equi-spaced divisions on the double ordinate, say 0 to 8, and back again as shown.
- The height of each abscissa is given as the products of the two numbers that result - i.e. 0x8, 1x7, 2x6, etc.
- Set the height of the parabola vertex as required, and divide this into a number of equal parts up to the maximum resulting product (i.e. 16 in this example) - constructions used to create Scales are convenient ways of doing this.
- Sketch a fair curve through the points (or use French Curves or a flexible strip for example)
|
|
Note:
Parabolas may also be drawn by more precise methods and the position of the Focus given. Tangents and Normals may also be drawn if needed - see Conics for more details.