Polygons: Difference between revisions
From DT Online
mNo edit summary |
mNo edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__TOC__ | |||
=====Description===== | |||
Drawing regular [https://en.wikipedia.org/wiki/Polygon '''Polygons'''] is now most easily accomplished using modern [https://en.wikipedia.org/wiki/Technical_drawing '''drafting'''] aids and [https://en.wikipedia.org/wiki/Computer-aided_design '''Computer Aided Design'''] tools. But there are occasions when it is useful to have an understanding of some basic constructions using just rule and compasses ''(or pegs and pieces of string)''. Examples might include large scale work for stage sets or carnival floats, or on-site work for buildings, playgrounds, sports fields and gardens. | Drawing regular [https://en.wikipedia.org/wiki/Polygon '''Polygons'''] is now most easily accomplished using modern [https://en.wikipedia.org/wiki/Technical_drawing '''drafting'''] aids and [https://en.wikipedia.org/wiki/Computer-aided_design '''Computer Aided Design'''] tools. But there are occasions when it is useful to have an understanding of some basic constructions using just rule and compasses ''(or pegs and pieces of string)''. Examples might include large scale work for stage sets or carnival floats, or on-site work for buildings, playgrounds, sports fields and gardens. | ||
| Line 11: | Line 16: | ||
</span> | </span> | ||
---- | ---- | ||
=====Constructions===== | |||
{| cellpadding="5" | {| cellpadding="5" | ||
| Line 25: | Line 32: | ||
* Draw a line of length equal to the length of side required. | * Draw a line of length equal to the length of side required. | ||
* From one end of the line construct a perpendicular - (see '''[[Basic Constructions]]'''). | * From one end of the line construct a perpendicular - (see '''[[Basic Constructions]]'''). | ||
* Set the line length as a radius and strike an arc along the | * Set the line length as a radius and strike an arc along the perpendicular to find the second side of the square. | ||
* Keep the same radius and strike arcs from the ends of the two adjacent sides as shown | * Keep the same radius and strike arcs from the ends of the two adjacent sides as shown | ||
* Joining to where the two arcs intersect provides the remaining two sides. | * Joining to where the two arcs intersect provides the remaining two sides. | ||
| Line 41: | Line 48: | ||
---- | ---- | ||
<span style="color: green">'''Note:''' | <span style="color: green">'''Note:''' | ||
Polygons with odd numbered sides have an apex at top centre and this can be used for greater accuracy as an | Polygons with odd numbered sides have an apex at top centre and this can be used for greater accuracy as an alternative starting point, or as check, when stepping off sides round the circle . | ||
</span> | </span> | ||
---- | ---- | ||
<span style="color: green">'''Note:''' | <span style="color: green">'''Note:''' | ||
This construction may be used for other polygons by stepping off an appropriate number of sides around the semi-circle - but in all cases always start by drawing a | This construction may be used for other polygons by stepping off an appropriate number of sides around the semi-circle - but in all cases always start by drawing a line through the 2nd division to establish the circumscribing circle centre. | ||
</span> | </span> | ||
---- | ---- | ||
| Line 58: | Line 65: | ||
---- | ---- | ||
<span style="color: green">'''Note:''' | <span style="color: green">'''Note:''' | ||
Polygons with even numbers of sides have diagonals | Polygons with even numbers of sides have diagonals parallel to the sides and this can be used as a check on accuracy | ||
</span> | </span> | ||
---- | ---- | ||
| Line 64: | Line 71: | ||
| [[File:CompassHex.png|250px|right]] | | [[File:CompassHex.png|250px|right]] | ||
|- | |- | ||
| '''Septagon''' | | '''Heptagon (aka Septagon)''' | ||
| <span style="color:#B00000"> | | <span style="color:#B00000"> | ||
* Draw a line of length equal to the length of side required and construct its perpendicular bisector - (see '''[[Basic Constructions]]'''). | * Draw a line of length equal to the length of side required and construct its perpendicular bisector - (see '''[[Basic Constructions]]'''). | ||
| Line 72: | Line 79: | ||
---- | ---- | ||
<span style="color: green">'''Note:''' | <span style="color: green">'''Note:''' | ||
A circle centred here would circumscribe a pentagon and provides an alternative construction. | |||
</span> | </span> | ||
---- | ---- | ||
* Set radius to half the distance between c4 and c6 and step off above c6 to create c7 - the centre of a circle which circumscribes a | * Set radius to half the distance between c4 and c6 and step off above c6 to create c7 - the centre of a circle which circumscribes a Heptagon ''(aka Septagon)'' | ||
* Set radius to the length of side and step off round the circle. | * Set radius to the length of side and step off round the circle. | ||
</span> | </span> | ||
| Line 93: | Line 100: | ||
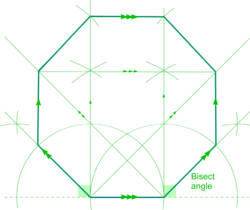
| [[File:CompassOctagon.png|250px|right]] | | [[File:CompassOctagon.png|250px|right]] | ||
|} | |} | ||
{{Drawing Instruments Buyers Guide}} | |||
[[Category:Secondary]] | [[Category:Secondary]] | ||
[[Category:Geometry]] | [[Category:Geometry]] | ||
Latest revision as of 10:04, 7 June 2018
Description
Drawing regular Polygons is now most easily accomplished using modern drafting aids and Computer Aided Design tools. But there are occasions when it is useful to have an understanding of some basic constructions using just rule and compasses (or pegs and pieces of string). Examples might include large scale work for stage sets or carnival floats, or on-site work for buildings, playgrounds, sports fields and gardens.
The following examples are limited to constructions of regular polygons. Irregular polygon construction may be achieved using a process of triangulation, vectors, coordinates or plotting points on a matrix for example. Some other polygons (e.g. Cyclic Quadlitateral) have particular properties which can be helpful to know when constructing them.
See also the YouTube video All the possible polygons!. This shows how all regular polygons can be constructed using classical geometry techniques
Note: Some constructions on the YouTube video may be different to those described below - there are several methods of construction possible for most regular polygons.
Constructions
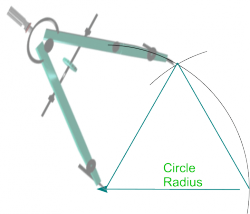
| Equilateral Triangle |
|
|
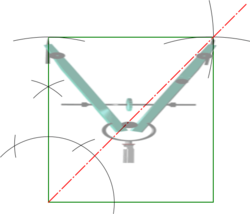
| Square |
|
|
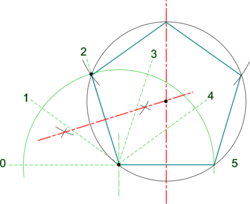
| Pentagon |
Note: Polygons with odd numbered sides have an apex at top centre and this can be used for greater accuracy as an alternative starting point, or as check, when stepping off sides round the circle . Note: This construction may be used for other polygons by stepping off an appropriate number of sides around the semi-circle - but in all cases always start by drawing a line through the 2nd division to establish the circumscribing circle centre.
|
|
| Hexagon |
Note: Polygons with even numbers of sides have diagonals parallel to the sides and this can be used as a check on accuracy
|
|
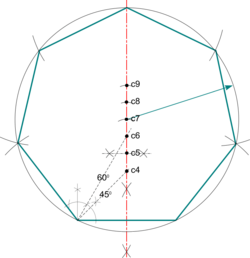
| Heptagon (aka Septagon) |
Note: A circle centred here would circumscribe a pentagon and provides an alternative construction.
|
|
| Octagon |
|