Tangents and Normals: Difference between revisions
From DT Online
(Added 'To construct a Tangent to a Circle from a point outside its circumference') |
(Added construction of tangents to an ellipse) |
||
| Line 12: | Line 12: | ||
<hr /> | <hr /> | ||
===== Construction of Tangents to an Ellipse ===== | ===== Construction of Tangents to an Ellipse ===== | ||
'''To construct a Tangent to an Ellipse from any point on the curve:''' | |||
* Join the point to each of the two Foci as shown and bisect the angle found between the two lines. | |||
* The bisector is the Normal and a Tangent may be drawn at right angles to it. | |||
'''To construct a Tangent to an Ellipse from any point outside the curve:''' | |||
* Strike an arc with the point as centre and radius equal to its distance from the Focus as shown. | |||
* Strike a second arc with the second Focus as centre and radius set to equal the Major Axis. | |||
* Join the points of intersection of the two arcs to the second Focus as shown. | |||
* Where the two lines intersect the curve give the two Points of Tangency. | |||
* Join the point to these Points of Tangency to produce the two possible Tangents and their Normals may be drawn at right angles to them. | |||
{| | {| | ||
|- | |- | ||
Revision as of 07:23, 8 April 2015
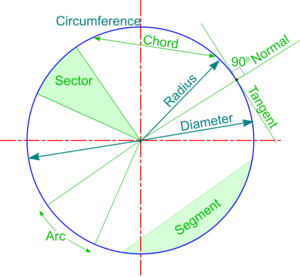
Tangents are lines just touching a given curve and its Normal is a line perpendicular to it at the point of contact (or point of Tangency).
Taking the common case of a Circle, the Normal to a Tangent from a point P on the circumference is a line joining the point to the circle centre - and the Tangent is at right angles to the Normal. This forms the basis for methods of constructing Tangents such that the Point of Tangency is given accurately.
To construct a Tangent to a Circle from a point outside its circumference:
- Join the point to the circle centre.
- Draw a semi-circle on this line as the diameter.
- The Point of Contact (or Tangency) for the Tangent is where the semi-cicle intersects the circle and its Normal joins this point to the circle centre (angle in semi-circle).
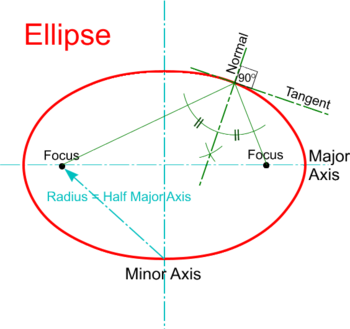
Construction of Tangents to an Ellipse
To construct a Tangent to an Ellipse from any point on the curve:
- Join the point to each of the two Foci as shown and bisect the angle found between the two lines.
- The bisector is the Normal and a Tangent may be drawn at right angles to it.
To construct a Tangent to an Ellipse from any point outside the curve:
- Strike an arc with the point as centre and radius equal to its distance from the Focus as shown.
- Strike a second arc with the second Focus as centre and radius set to equal the Major Axis.
- Join the points of intersection of the two arcs to the second Focus as shown.
- Where the two lines intersect the curve give the two Points of Tangency.
- Join the point to these Points of Tangency to produce the two possible Tangents and their Normals may be drawn at right angles to them.
|

|
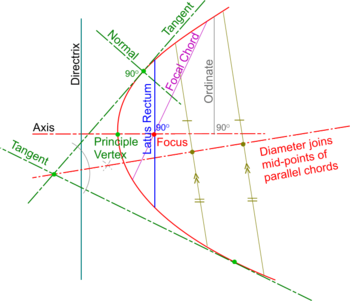
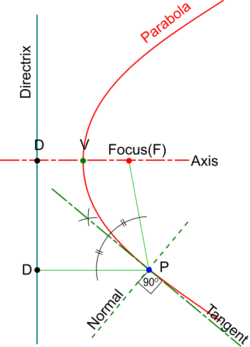
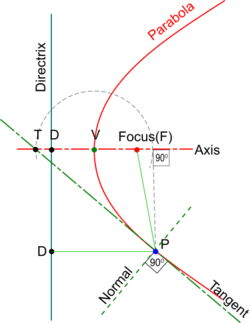
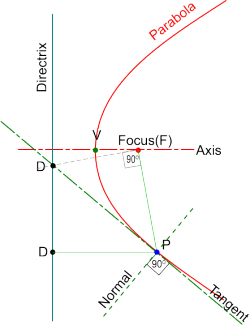
Construction of Tangents to a Parabola
|
|
|
Tangents and Normals are two terms used to describe properties of all conics. Other common properties are as follows:
- A Chord is a straight line joining two points on the curve.
- A Focal Chord is a Chord which passses through the Focus
- The mid-points of parallel Chords lie in a straight line called a Diameter
- A perpendicular from a point on the Axis is called an Ordinate and if it goes straight across to the other side, it is a Double Ordinate.
- The Double Ordinate through the Focus is the Latus Rectum (translates from Latin as ‘The Right Side’).
- A Normal to any conic is at right angles to a Tangent at the Point of Contact