Beam Deflection: Difference between revisions
From DT Online
m (Added bullets) |
(Added deflected beam diagram) |
||
| Line 3: | Line 3: | ||
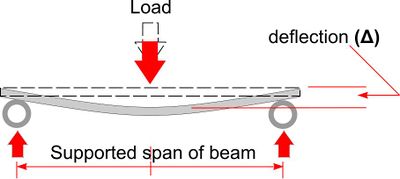
The equation opposite gives [http://en.wikipedia.org/wiki/Deflection_%28engineering%29#Beam_deflection_for_various_loads_and_supports '''Deflection (Δ)'''] of a simply supported beam loaded in the centre. | The equation opposite gives [http://en.wikipedia.org/wiki/Deflection_%28engineering%29#Beam_deflection_for_various_loads_and_supports '''Deflection (Δ)'''] of a simply supported beam loaded in the centre. | ||
[[File:WhiteSpace.jpg|300px|right]] | |||
[[File:BeamDeflectionLabelled.jpg|400px|right]] | |||
'''Where''': | '''Where''': | ||
Revision as of 11:58, 7 November 2014
The deflection of a beam under load may be measured using a dial gauge for example but may also be calculated.
The equation opposite gives Deflection (Δ) of a simply supported beam loaded in the centre.
Where:
- W = Load
- L = Span
- E = Young's Modulus ( - a measure of how stiff the materials is)
- I = Moment of Inertia ( - a measure of the capacity of a cross section to resist bending)