Tangents and Normals: Difference between revisions
From DT Online
mNo edit summary |
Added Template |
||
| (10 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:CircleParts.png | | [[File:CircleParts.png |300px|right]] | ||
__TOC__ | |||
===== Description===== | |||
[https://en.wikipedia.org/wiki/Tangent '''Tangents'''] are lines ''just touching'' a given curve and its [https://en.wikipedia.org/wiki/Normal_%28geometry%29 '''Normal'''] is a line perpendicular to it at the point of contact ''(or point of '''Tangency''')''. | [https://en.wikipedia.org/wiki/Tangent '''Tangents'''] are lines ''just touching'' a given curve and its [https://en.wikipedia.org/wiki/Normal_%28geometry%29 '''Normal'''] is a line perpendicular to it at the point of contact ''(or point of '''Tangency''')''. | ||
Taking the common case of a '''[[Circles|Circle]]''', the '''Normal''' to a '''Tangent''' from a point '''P''' on the circumference is a line joining the point to the circle centre - and the '''Tangent''' is at right angles to the '''Normal'''. This forms the basis for methods of constructing '''Tangents''' such that the '''Point of Tangency''' is given accurately. | Taking the common case of a '''[[Circles|Circle]]''', the '''Normal''' to a '''Tangent''' from a point '''P''' on the circumference is a line joining the point to the circle centre - and the '''Tangent''' is at right angles to the '''Normal'''. This forms the basis for methods of constructing '''Tangents''' such that the '''Point of Tangency''' is given accurately.<div style="clear: both;"></div> | ||
<hr /> | |||
===== To construct a Tangent to a Circle from a point outside its circumference: ===== | |||
[[File:TangentPointCircle.png |350px|right]] | |||
* Join the point to the circle centre. | |||
* Draw a semi-circle on this line as the diameter. | |||
* The Point of Contact (''or Tangency)'' for the Tangent is where the semi-cicle intersects the circle and its Normal joins this point to the circle centre ''[[Circles|(angle in semi-circle)]]''. | |||
<hr /> | |||
===== Construction of Tangents to an Ellipse ===== | |||
'''To construct a Tangent to an Ellipse from any point on the curve:''' | |||
* Join the point to each of the two Foci as shown and bisect the angle found between the two lines. | |||
* The bisector is the Normal and a Tangent may be drawn at right angles to it. | |||
'''To construct a Tangent to an Ellipse from any point outside the curve:''' | |||
* Strike an arc with the point as centre and radius equal to its distance from the Focus as shown. | |||
* Strike a second arc with the second Focus as centre and radius set to equal the Major Axis. | |||
* Join the points of intersection of the two arcs to the second Focus as shown. | |||
* Where the two lines intersect the curve give the two Points of Tangency. | |||
* Join the point to these Points of Tangency to produce the two possible Tangents and their Normals may be drawn at right angles to them. | |||
{| | |||
|- | |||
| [[File:Tangent-Ellipse.png |350px]] | |||
| [[File:Tangent-PointEllipse.png |350px]] | |||
|} | |||
<hr /> | |||
===== Construction of Tangents to a Parabola ===== | |||
'''Three methods to construct a Tangent to a point on the Parabola''' | |||
'''Method 1.''' | |||
* Join the point to the Focus and draw from it a perpendicular to the Directrix. | |||
* The bisector of the two lines created is the Tangent and its Normal may be constructed at right angles to it. | |||
'''Method 2.''' | |||
* Draw a line from the point perpendicular to the Axis ''(i.e. an Ordinate)'' | |||
* With the Vertex as centre and radius the distance from the Vertex to where the Ordinate intersects the Axis, draw a semi-circle. | |||
* Draw the Tangent to the point from where the semi-circle cuts the Axis as shown and its Normal may be constructed at right angles to it. | |||
'''Method 3.''' | |||
* Join the point to the Focus construct a line at right angles to it from the Focus. | |||
* Draw the Tangent to the point from the line's intersection the Directrix and its Normal may be constructed at right angles to it. | |||
{| | |||
|- | |||
| [[File:Tangent-Parabola.png|250px]] | |||
| [[File:Tangent-Parabola2.png|250px]] | |||
| [[File:Tangent-Parabola3.png|250px]] | |||
|} | |||
<hr /> | |||
[[File:Tangent-PointParabola.png|200px|right]] | |||
=====To construct a Tangent from a point outside the Parabola ===== | |||
* Join the point (P) to the Focus(F) and using this as diameter, decribe a circle. | |||
* Draw Tangent at the Vertex (V) perpendicular to the Axis to intersect the circle circumference in X and Y. | |||
* Join PX and PY and produce both to touch the Parabola generating the two Tangents as shown. | |||
* To draw a Normal, produce a Tangent ''(e.g. YP)'' to meet the Directrix in D and join D to the Focus(F). | |||
* A line drawn perpendicular to DF will intersect the Parabola at a Point of Tangency(T). | |||
* Construct a perpendicular to the Tangent from its Point of Tangency(T) to create its Normal. | |||
<hr /> | |||
[[File:ConicsProperties.png |350px|right]] | |||
===== Other terms common to all conics ===== | |||
'''Tangents''' and '''Normals''' are two terms used to describe properties of all conics. Other common properties are as follows: | |||
* A '''Chord''' is a straight line joining two points on the curve. | |||
* A '''Focal Chord''' is a Chord which passses through the '''Focus''' | |||
* The mid-points of parallel Chords lie in a straight line called a '''Diameter''' | |||
* A perpendicular from a point on the '''Axis''' is called an '''Ordinate''' and if it goes straight across to the other side, it is a '''Double Ordinate'''. | |||
* The Double Ordinate through the Focus is the '''Latus Rectum''' ''(translates from Latin as ‘The Right Side’)''. | |||
* A '''Normal''' to any conic is at right angles to a '''Tangent''' at the '''Point of Contact''' | |||
{{Drawing Instruments Buyers Guide}} | |||
[[Category:Secondary]] | |||
[[Category:Geometry]] | |||
Latest revision as of 19:25, 2 June 2016
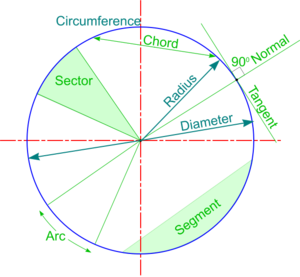
Description
Tangents are lines just touching a given curve and its Normal is a line perpendicular to it at the point of contact (or point of Tangency).
Taking the common case of a Circle, the Normal to a Tangent from a point P on the circumference is a line joining the point to the circle centre - and the Tangent is at right angles to the Normal. This forms the basis for methods of constructing Tangents such that the Point of Tangency is given accurately.
To construct a Tangent to a Circle from a point outside its circumference:

- Join the point to the circle centre.
- Draw a semi-circle on this line as the diameter.
- The Point of Contact (or Tangency) for the Tangent is where the semi-cicle intersects the circle and its Normal joins this point to the circle centre (angle in semi-circle).
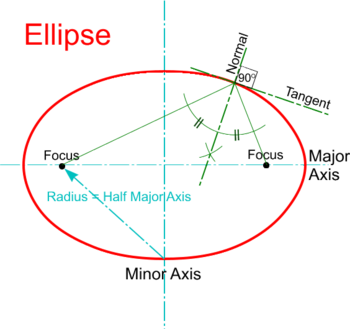
Construction of Tangents to an Ellipse
To construct a Tangent to an Ellipse from any point on the curve:
- Join the point to each of the two Foci as shown and bisect the angle found between the two lines.
- The bisector is the Normal and a Tangent may be drawn at right angles to it.
To construct a Tangent to an Ellipse from any point outside the curve:
- Strike an arc with the point as centre and radius equal to its distance from the Focus as shown.
- Strike a second arc with the second Focus as centre and radius set to equal the Major Axis.
- Join the points of intersection of the two arcs to the second Focus as shown.
- Where the two lines intersect the curve give the two Points of Tangency.
- Join the point to these Points of Tangency to produce the two possible Tangents and their Normals may be drawn at right angles to them.
|

|
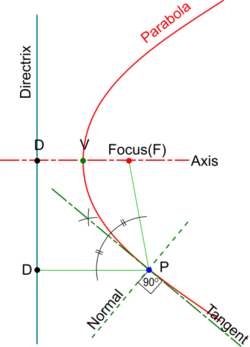
Construction of Tangents to a Parabola
Three methods to construct a Tangent to a point on the Parabola
Method 1.
- Join the point to the Focus and draw from it a perpendicular to the Directrix.
- The bisector of the two lines created is the Tangent and its Normal may be constructed at right angles to it.
Method 2.
- Draw a line from the point perpendicular to the Axis (i.e. an Ordinate)
- With the Vertex as centre and radius the distance from the Vertex to where the Ordinate intersects the Axis, draw a semi-circle.
- Draw the Tangent to the point from where the semi-circle cuts the Axis as shown and its Normal may be constructed at right angles to it.
Method 3.
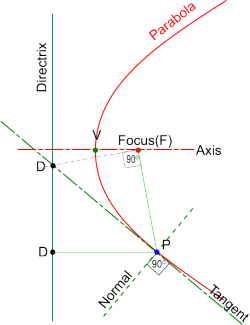
- Join the point to the Focus construct a line at right angles to it from the Focus.
- Draw the Tangent to the point from the line's intersection the Directrix and its Normal may be constructed at right angles to it.
|
|
|
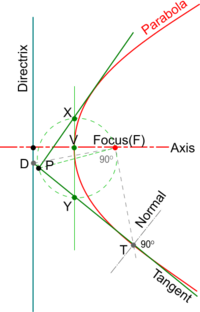
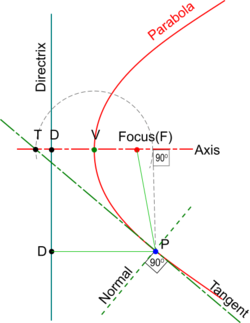
To construct a Tangent from a point outside the Parabola
- Join the point (P) to the Focus(F) and using this as diameter, decribe a circle.
- Draw Tangent at the Vertex (V) perpendicular to the Axis to intersect the circle circumference in X and Y.
- Join PX and PY and produce both to touch the Parabola generating the two Tangents as shown.
- To draw a Normal, produce a Tangent (e.g. YP) to meet the Directrix in D and join D to the Focus(F).
- A line drawn perpendicular to DF will intersect the Parabola at a Point of Tangency(T).
- Construct a perpendicular to the Tangent from its Point of Tangency(T) to create its Normal.
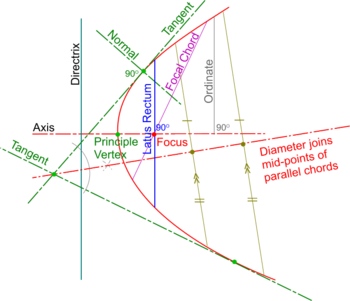
Other terms common to all conics
Tangents and Normals are two terms used to describe properties of all conics. Other common properties are as follows:
- A Chord is a straight line joining two points on the curve.
- A Focal Chord is a Chord which passses through the Focus
- The mid-points of parallel Chords lie in a straight line called a Diameter
- A perpendicular from a point on the Axis is called an Ordinate and if it goes straight across to the other side, it is a Double Ordinate.
- The Double Ordinate through the Focus is the Latus Rectum (translates from Latin as ‘The Right Side’).
- A Normal to any conic is at right angles to a Tangent at the Point of Contact









