Beam Deflection: Difference between revisions
From DT Online
Added deflected beam diagram |
mNo edit summary |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
The deflection of a beam under load may be measured using a dial gauge for example but may also be calculated. | The deflection of a beam under load may be measured using a dial gauge for example but may also be calculated. | ||
The equation opposite gives [http://en.wikipedia.org/wiki/Deflection_%28engineering%29 | |||
[[File:DeflectionCalc.png|300px|right]] | |||
The equation opposite gives [http://en.wikipedia.org/wiki/Deflection_%28engineering%29 '''Deflection (Δ)'''] of a simply supported beam loaded in the centre. | |||
[[File:BeamDeflectionLabelled.jpg|400px|right]] | [[File:BeamDeflectionLabelled.jpg|400px|right]] | ||
'''Where''': | '''Where''': | ||
| Line 9: | Line 11: | ||
* W = Load | * W = Load | ||
* L = Span | * L = Span | ||
* E = | * E = '''[[Young's Modulus]]''' ''( - a measure of how stiff the materials is)'' | ||
* I = '''[[Moment of Inertia]]''' ''( - a measure of the capacity of a cross section to resist bending)'' | * I = '''[[Moment of Inertia]]''' ''( - a measure of the capacity of a cross section to resist '''[[Bending Strength|bending]]''')'' | ||
---- | |||
[[Category:Secondary]] | |||
[[Category:Beams]] | |||
Latest revision as of 10:22, 1 March 2017
The deflection of a beam under load may be measured using a dial gauge for example but may also be calculated.

The equation opposite gives Deflection (Δ) of a simply supported beam loaded in the centre.
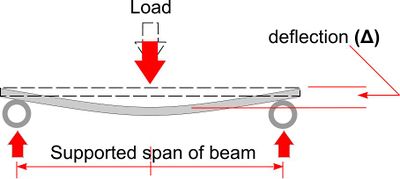
Where:
- W = Load
- L = Span
- E = Young's Modulus ( - a measure of how stiff the materials is)
- I = Moment of Inertia ( - a measure of the capacity of a cross section to resist bending)