Loci: Difference between revisions
From DT Online
(Added Template) |
mNo edit summary |
||
| Line 7: | Line 7: | ||
For example: the locus of all points a set distance from another point is a circle; the locus of all points | For example: the locus of all points a set distance from another point is a circle; the locus of all points equidistant from the ends of a line is the [[Basic Constructions|perpendicular bisector]] of the line; and the locus of all points a set distance from a given line are lines parallel to it ''(or an oval if the locus continues round the ends of the line)'' | ||
More practically it sometimes necessary to know the path traced by the ends of pieces of machinery to check clearances, estimate the velocities at different parts of a linkage ''(perhaps to calculate momentum)'' or to design guarding for example. The general method is to draw the linkage or mechanism in several ‘freeze frame’ positions then draw a smooth curve through the plotted points. | More practically it is sometimes necessary to know the path traced by the ends of pieces of machinery to check clearances, estimate the velocities at different parts of a linkage ''(perhaps to calculate momentum)'' or to design guarding for example. The general method is to draw the linkage or mechanism in several ‘freeze frame’ positions then draw a smooth curve through the plotted points. | ||
| Line 22: | Line 22: | ||
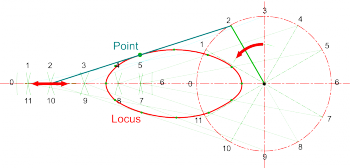
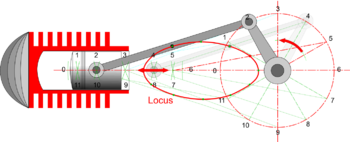
* Number the crank positions and, with radius set to the length of the connecting rod, strike arcs from each position along the horizontal line which the piston is constrained to slide along. | * Number the crank positions and, with radius set to the length of the connecting rod, strike arcs from each position along the horizontal line which the piston is constrained to slide along. | ||
* If the requirement is for the locus of the centre of the connecting rod, then mark these points on each position and join with a smooth curve as shown. | * If the requirement is for the locus of the centre of the connecting rod, then mark these points on each position and join with a smooth curve as shown. | ||
* It may sometimes be | * It may sometimes be necessary to draw in additional details of the mechanisms, to test clearances for example. | ||
* Loci on parts of other mechanisms can be plotted using a similar process - i.e. draw the mechanism in different positions and connect plotted points to create the locus. | * Loci on parts of other mechanisms can be plotted using a similar process - i.e. draw the mechanism in different positions and connect plotted points to create the locus. | ||
</span> | </span> | ||
Revision as of 08:54, 14 March 2017
Description
The Locus of a Point is the path traced by a point as it moves in accordance with set conditions and constraints. The plural of Locus is Loci.
For example: the locus of all points a set distance from another point is a circle; the locus of all points equidistant from the ends of a line is the perpendicular bisector of the line; and the locus of all points a set distance from a given line are lines parallel to it (or an oval if the locus continues round the ends of the line)
More practically it is sometimes necessary to know the path traced by the ends of pieces of machinery to check clearances, estimate the velocities at different parts of a linkage (perhaps to calculate momentum) or to design guarding for example. The general method is to draw the linkage or mechanism in several ‘freeze frame’ positions then draw a smooth curve through the plotted points.
Constructions
| Plotting Loci on a Crank and Slider Mechanism |
|
|