Ellipse: Difference between revisions
From DT Online
(Created Ellipse) |
(Added Template) |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__TOC__ | |||
=====Description===== | |||
An [https://en.wikipedia.org/wiki/Ellipse '''Ellipse'''] is a '''[[Conic Sections|Conic Section]]''' and has the appearance of a circle which has been squashed slightly. Unlike a circle, which has a single '''Diameter''', the ellipse has a '''Major Axis''' and a '''Minor Axis'''. The shape of an ellipse is sometimes mistakenly referred to as an '''''oval''''', but an oval is the shape of a rectangle with two semi-circular ends - like a running track for example. | An [https://en.wikipedia.org/wiki/Ellipse '''Ellipse'''] is a '''[[Conic Sections|Conic Section]]''' and has the appearance of a circle which has been squashed slightly. Unlike a circle, which has a single '''Diameter''', the ellipse has a '''Major Axis''' and a '''Minor Axis'''. The shape of an ellipse is sometimes mistakenly referred to as an '''''oval''''', but an oval is the shape of a rectangle with two semi-circular ends - like a running track for example. | ||
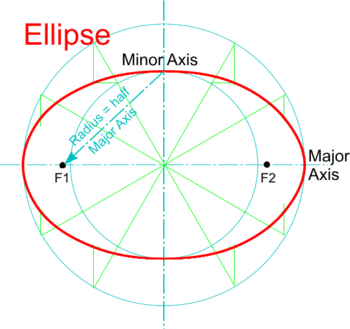
The ellipse has two points of ''focus'', or ''''' | The ellipse has two points of ''focus'', or '''''foci'''''. These can be found on the Major Axis by using half its length as a radius, and striking an arc centred on one end of the Minor Axis as shown. | ||
=====Constructions===== | |||
{| cellpadding="5" | {| cellpadding="5" | ||
| Line 9: | Line 16: | ||
| <span style="color:#B00000"> | | <span style="color:#B00000"> | ||
* Draw two circles from the same centre: one with its diameter equal to the Major Axis, and one equal to the Minor Axis. | * Draw two circles from the same centre: one with its diameter equal to the Major Axis, and one equal to the Minor Axis. | ||
* Divide the circles into a number of segments | * Divide the circles into a number of segments ''(say, 12 as shown)''. | ||
* Project vertically from where the radial lines intersect the outer circle and .horizontally from where they meet the inner circle ''(or vice versa)'' | * Project vertically from where the radial lines intersect the outer circle and .horizontally from where they meet the inner circle ''(or vice versa)'' | ||
* Points on the ellipse can be found where each pair of projection lines meet as shown. | * Points on the ellipse can be found where each pair of projection lines meet as shown. | ||
* Sketch a fair curve through the points ''(or use [https://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [https://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)'' | * Sketch a fair curve through the points ''(or use [https://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [https://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)'' | ||
| [[File: | | [[File:CirclesEllipse.png|350px|right]] | ||
|- | |- | ||
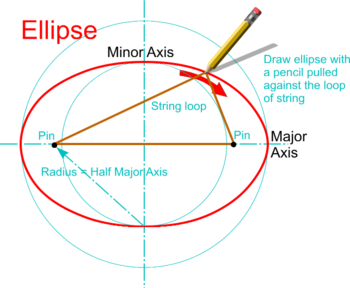
| '''Drawing an Ellipse using a loop of string''' | | '''Drawing an Ellipse using a loop of string''' | ||
| <span style="color:#B00000"> | | <span style="color:#B00000"> | ||
* A property of the ellipse is that the sum of the distances from any point on the curve to each of its two | * A property of the ellipse is that the sum of the distances from any point on the curve to each of its two Foci is constant. | ||
* Start by setting compasses, or similar, to half the Major Axis and strike arcs on it from one end of the Minor Axis as shown. | * Start by setting compasses, or similar, to half the Major Axis and strike arcs on it from one end of the Minor Axis as shown. | ||
* The intersections found by the two arcs are the Focii of the ellipse. | * The intersections found by the two arcs are the Focii of the ellipse. | ||
* Place the drawing on a board and insert pins at each | * Place the drawing on a board and insert pins at each Foci then make a loop of string to go around them and reach the end of the Minor Axis when pulled tight. | ||
* Hold a pencil inside the loop and keep the string tight as the pencil is pulled around to draw the complete ellipse as shown.</span> | * Hold a pencil inside the loop and keep the string tight as the pencil is pulled around to draw the complete ellipse as shown.</span> | ||
| [[File: | | [[File:StringEllipse.png|350px|right]] | ||
|} | |} | ||
---- | ---- | ||
<span style="color: green">'''Note:''' | <span style="color: green">'''Note:''' | ||
Ellipses may also be drawn by more precise methods with '''Tangents''' and '''Normals''' drawn if needed - see '''[[ | Ellipses may also be drawn by more precise methods and with '''[[Tangents and Normals|Tangents]]''' and '''[[Tangents and Normals|Normals]]''' drawn if needed - see '''[[Conics]]''' for more details. | ||
</span> | </span> | ||
---- | ---- | ||
{{Drawing Instruments Buyers Guide}} | |||
Latest revision as of 19:02, 2 June 2016
Description
An Ellipse is a Conic Section and has the appearance of a circle which has been squashed slightly. Unlike a circle, which has a single Diameter, the ellipse has a Major Axis and a Minor Axis. The shape of an ellipse is sometimes mistakenly referred to as an oval, but an oval is the shape of a rectangle with two semi-circular ends - like a running track for example.
The ellipse has two points of focus, or foci. These can be found on the Major Axis by using half its length as a radius, and striking an arc centred on one end of the Minor Axis as shown.
Constructions
| Drawing an Ellipse using Concentric Circles |
|
|
| Drawing an Ellipse using a loop of string |
|
Note: Ellipses may also be drawn by more precise methods and with Tangents and Normals drawn if needed - see Conics for more details.