Parabola: Difference between revisions
From DT Online
m Corrected link |
mNo edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
__TOC__ | |||
An important characteristic of a parabola-shaped reflector is that any beam of light, sound or other energy which enters travelling parallel to its main axis is reflected through a single point called its '''''focus'''''. Conversely, light that originates from a point source at the focus is reflected into a parallel beam. This makes parabolic forms ''(i.e. [ | =====Description===== | ||
A [http://en.wikipedia.org/wiki/Parabola '''Parabola'''] is a '''[[Conic Sections|Conic Section]]''' and describes the path ''(or trajectory)'' taken by a ball as it is thrown in the air. | |||
An important characteristic of a parabola-shaped reflector is that any beam of light, sound or other energy which enters travelling parallel to its main axis is reflected through a single point called its '''''focus'''''. Conversely, light that originates from a point source at the focus is reflected into a parallel beam. This makes parabolic forms ''(i.e. [http://en.wikipedia.org/wiki/Paraboloid '''parabloids'''])'' very useful for microphones and spotlight reflectors for example. | |||
Parabolas can be drawn as the graph of '''y=x<sup>2</sup>''' but there are other ways of drawing a parabola which exploit its various mathematical properties. | Parabolas can be drawn as the graph of '''y=x<sup>2</sup>''' but there are other ways of drawing a parabola which exploit its various mathematical properties. | ||
=====Constructions===== | |||
{| cellpadding="5" | {| cellpadding="5" | ||
| Line 15: | Line 22: | ||
* Draw vertical lines through all the divisions along the base then radial lines from the top centre ''(which will become the '''Vertex''')'' to each of the vertical divisions to intersect them - i.e. Point 1 is where vertical Line 1 is intersected by Radial line 1. | * Draw vertical lines through all the divisions along the base then radial lines from the top centre ''(which will become the '''Vertex''')'' to each of the vertical divisions to intersect them - i.e. Point 1 is where vertical Line 1 is intersected by Radial line 1. | ||
* Repeat the process for the right hand half of the parabola but note that the base divisions will now be numbered right to left. | * Repeat the process for the right hand half of the parabola but note that the base divisions will now be numbered right to left. | ||
* Sketch a fair curve through the points ''(or use [ | * Sketch a fair curve through the points ''(or use [http://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [http://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)''</span> | ||
| [[File:Parabola.png|350px|right]] | | [[File:Parabola.png|350px|right]] | ||
|- | |- | ||
| [ | | [http://en.wikipedia.org/wiki/String_art '''Curve Stitching'''] | ||
| <span style="color:#B00000"> | | <span style="color:#B00000"> | ||
*'''Curve Stitching''''' (or '''String Art''')'' is a craft technique used to create patterns from parabolas and other curves by sewing threads between points along two intersecting lines. | *'''Curve Stitching''''' (or '''String Art''')'' is a craft technique used to create patterns from parabolas and other curves by sewing threads between points along two intersecting lines. | ||
* The technique was invented by [ | * The technique was invented by [http://en.wikipedia.org/wiki/Mary_Everest_Boole '''Mary Everest Boole'''] at the end of the 19th Century to make maths more interesting to children and became very popular during the 1960's to decorate gift cards for example. | ||
* Instead of sewing threads, lines can be drawn between the points and a parabola created by sketching a fair curve to touch the lines ''(or use [ | * Instead of sewing threads, lines can be drawn between the points and a parabola created by sketching a fair curve to touch the lines ''(or use [http://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [http://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)''</span> | ||
---- | ---- | ||
<span style="color: green">'''Note:''' | <span style="color: green">'''Note:''' | ||
The idea of creating curves using straight lines is put to practical use to design and build curved roofs and curve-sided towers and even bridges using straight pieces of material - see [ | The idea of creating curves using straight lines is put to practical use to design and build curved roofs and curve-sided towers and even bridges using straight pieces of material - see [http://en.wikipedia.org/wiki/Saddle_roof '''Saddle Roofs'''] and [http://en.wikipedia.org/wiki/Cooling_tower '''Cooling Towers''' or ][http://en.wikipedia.org/wiki/Hyperboloid_structure '''Hyperboloid structures'''] and [http://en.wikipedia.org/wiki/Mathematical_Bridge '''The Mathematical Bridge at Cambridge'''] for examples. | ||
</span> | </span> | ||
---- | ---- | ||
| [[File:ParabolaStitching.png|350px|right]] | | [[File:ParabolaStitching.png|350px|right]] | ||
|- | |- | ||
| '''Using measured [ | | '''Using measured [http://en.wikipedia.org/wiki/Abscissa Abscissae]''' | ||
| <span style="color:#B00000"> | | <span style="color:#B00000"> | ||
* A property of the parabola is that the '''abscissa''', that part of a diameter of a '''conic''' between its '''vertex''' and an '''ordinate''', is ''‘proportional to the product of the parts into which it divides the double ordinate’''. | * A property of the parabola is that the '''abscissa''', that part of a diameter of a '''conic''' between its '''vertex''' and an '''ordinate''', is ''‘proportional to the product of the parts into which it divides the double ordinate’''. | ||
| Line 37: | Line 44: | ||
* The height of each abscissa is given as the products of the two numbers that result - i.e. 0x8, 1x7, 2x6, etc. | * The height of each abscissa is given as the products of the two numbers that result - i.e. 0x8, 1x7, 2x6, etc. | ||
* Set the height of the parabola vertex as required, and divide this into a number of equal parts up to the maximum resulting product ''(i.e. 16 in this example)'' - constructions used to create '''[[Scales]]''' are convenient ways of doing this. | * Set the height of the parabola vertex as required, and divide this into a number of equal parts up to the maximum resulting product ''(i.e. 16 in this example)'' - constructions used to create '''[[Scales]]''' are convenient ways of doing this. | ||
* Sketch a fair curve through the points ''(or use [ | * Sketch a fair curve through the points ''(or use [http://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [http://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)''</span> | ||
| [[File:ParabolaAbscissa.png|350px|right]] | | [[File:ParabolaAbscissa.png|350px|right]] | ||
|} | |} | ||
---- | ---- | ||
<span style="color: green">'''Note:''' | <span style="color: green">'''Note:''' | ||
Parabolas may also be drawn by more precise methods and the position of the '''Focus''' given. '''Tangents''' and '''Normals''' may also be drawn if needed - see '''[[ | Parabolas may also be drawn by more precise methods and the position of the '''[[Tangents and Normals|Focus]]''' given. '''[[Tangents and Normals|Tangents]]''' and '''[[Tangents and Normals|Normals]]''' may also be drawn if needed - see '''[[Conics]]''' for more details. | ||
</span> | </span> | ||
---- | ---- | ||
{{Drawing Instruments Buyers Guide}} | |||
Latest revision as of 12:07, 4 February 2017
Description
A Parabola is a Conic Section and describes the path (or trajectory) taken by a ball as it is thrown in the air.
An important characteristic of a parabola-shaped reflector is that any beam of light, sound or other energy which enters travelling parallel to its main axis is reflected through a single point called its focus. Conversely, light that originates from a point source at the focus is reflected into a parallel beam. This makes parabolic forms (i.e. parabloids) very useful for microphones and spotlight reflectors for example.
Parabolas can be drawn as the graph of y=x2 but there are other ways of drawing a parabola which exploit its various mathematical properties.
Constructions
| Drawing a Parabola within a Rectangle |
|
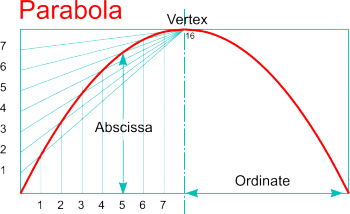 |
| Curve Stitching |
Note: The idea of creating curves using straight lines is put to practical use to design and build curved roofs and curve-sided towers and even bridges using straight pieces of material - see Saddle Roofs and Cooling Towers or Hyperboloid structures and The Mathematical Bridge at Cambridge for examples. |
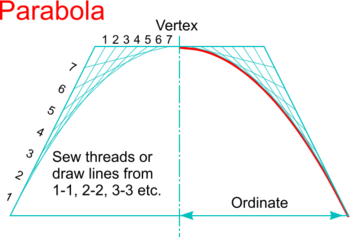 |
| Using measured Abscissae |
|
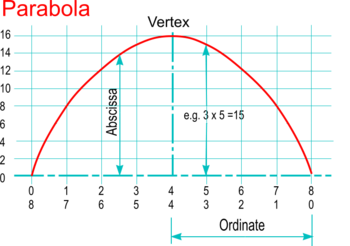 |
Note: Parabolas may also be drawn by more precise methods and the position of the Focus given. Tangents and Normals may also be drawn if needed - see Conics for more details.









