Conics: Difference between revisions
From DT Online
Created Conics |
Added Template |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Conics-Eccentricity.png|350px|right]] | [[File:Conics-Eccentricity.png|350px|right]] | ||
__TOC__ | |||
=====Description===== | |||
Early Greek mathematicians, and in particular [https://en.wikipedia.org/wiki/Apollonius_of_Perga '''Apollonius'''], provided most of our understanding of the properties of the three principle '''[[Conic Sections]]''', '''[[Ellipse]]''', '''[[Parabola]]''' and '''[[Conic Sections|Hyperbola]]''' ''(plus the circle as a fourth conic)''. | Early Greek mathematicians, and in particular [https://en.wikipedia.org/wiki/Apollonius_of_Perga '''Apollonius'''], provided most of our understanding of the properties of the three principle '''[[Conic Sections]]''', '''[[Ellipse]]''', '''[[Parabola]]''' and '''[[Conic Sections|Hyperbola]]''' ''(plus the circle as a fourth conic)''. | ||
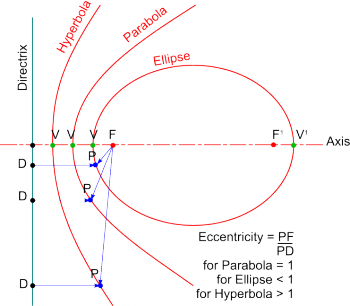
This work of Apollonius was extended by [https://en.wikipedia.org/wiki/Pappus_of_Alexandria '''Pappus of Alexandria'''] to describe Conic Sections in terms of a '''Focus''', a '''Directrix''' and the resulting [https://en.wikipedia.org/wiki/Eccentricity_%28mathematics%29 '''Eccentricity'''] for each conic ''(i.e. for any point on a conic section the ratio of its distance from the Focus to its distance from the Directrix is a constant known as the Eccentricity of the conic | This work of Apollonius was extended by [https://en.wikipedia.org/wiki/Pappus_of_Alexandria '''Pappus of Alexandria'''] to describe Conic Sections in terms of a '''Focus''', a '''Directrix''' and the resulting [https://en.wikipedia.org/wiki/Eccentricity_%28mathematics%29 '''Eccentricity'''] for each conic ''(i.e. for any point on a conic section the ratio of its distance from the Focus to its distance from the Directrix is a constant known as the '''Eccentricity''' of the conic - it is a measure of how far the conic deviates from being circular)''. | ||
=====Constructions===== | |||
Using this idea, any conic can be drawn as a '''[[Loci]]''' as follows: | Using this idea, any conic can be drawn as a '''[[Loci]]''' as follows: | ||
| Line 13: | Line 20: | ||
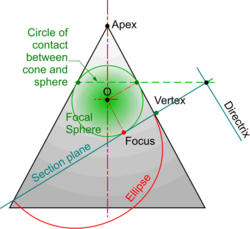
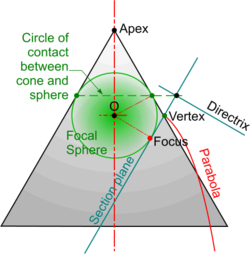
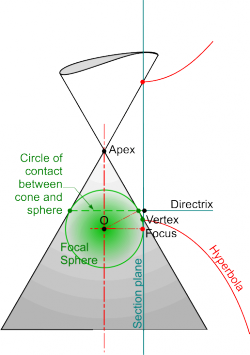
The derivation of these properties can be seen below. The starting point is the circular line of contact between a cone and a sphere placed inside it. The sphere is known as the '''Focal Sphere''' and where the circular line of contact projects on to the section plane gives the intersection between the '''Axis''' and the '''Directrix'''. The point of contact | The derivation of these properties can be seen below. The starting point is the circular line of contact between a cone and a sphere placed inside it. The sphere is known as the '''Focal Sphere''' and where the circular line of contact projects on to the section plane gives the intersection between the '''Axis''' and the '''Directrix'''. The point of contact, or '''''[[Tangents and Normals|tangency]]''''', between the sphere and the section plane is the '''Focus'''. The '''Vertex''' is the intersection between the section plane and the generating side of the cone. | ||
{| | {| | ||
|- | |- | ||
| Line 20: | Line 27: | ||
| [[File:FocusDirectrix-Hyperbola.png|250px]] | | [[File:FocusDirectrix-Hyperbola.png|250px]] | ||
|} | |} | ||
{{Drawing Instruments Buyers Guide}} | |||
[[Category:Secondary]] | |||
[[Category:Geometry]] | |||
Latest revision as of 18:58, 2 June 2016
Description
Early Greek mathematicians, and in particular Apollonius, provided most of our understanding of the properties of the three principle Conic Sections, Ellipse, Parabola and Hyperbola (plus the circle as a fourth conic).
This work of Apollonius was extended by Pappus of Alexandria to describe Conic Sections in terms of a Focus, a Directrix and the resulting Eccentricity for each conic (i.e. for any point on a conic section the ratio of its distance from the Focus to its distance from the Directrix is a constant known as the Eccentricity of the conic - it is a measure of how far the conic deviates from being circular).
Constructions
Using this idea, any conic can be drawn as a Loci as follows:
- Drawn a line to represent the main Axis.
- Draw a line perpendicular to the Axis to create the Directrix.
- Mark points along the Axis in the ratio of the Exccentricity - these plot the Vertex and Focus.
- Plot additional points on the conic such that the distances from the Focus and Directrix are in the ratio of the Eccentricity.
The derivation of these properties can be seen below. The starting point is the circular line of contact between a cone and a sphere placed inside it. The sphere is known as the Focal Sphere and where the circular line of contact projects on to the section plane gives the intersection between the Axis and the Directrix. The point of contact, or tangency, between the sphere and the section plane is the Focus. The Vertex is the intersection between the section plane and the generating side of the cone.
|
|
|









