Parabola: Difference between revisions
From DT Online
mNo edit summary |
(Changed Images) |
||
| Line 16: | Line 16: | ||
* Repeat the process for the right hand half of the parabola but note that the base divisions will now be numbered right to left. | * Repeat the process for the right hand half of the parabola but note that the base divisions will now be numbered right to left. | ||
* Sketch a fair curve through the points ''(or use [https://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [https://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)''</span> | * Sketch a fair curve through the points ''(or use [https://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [https://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)''</span> | ||
| [[File: | | [[File:Parabola.png|350px|right]] | ||
|- | |- | ||
| [https://en.wikipedia.org/wiki/String_art '''Curve Stitching'''] | | [https://en.wikipedia.org/wiki/String_art '''Curve Stitching'''] | ||
| Line 28: | Line 28: | ||
</span> | </span> | ||
---- | ---- | ||
| [[File: | | [[File:ParabolaStitching.png|350px|right]] | ||
|- | |- | ||
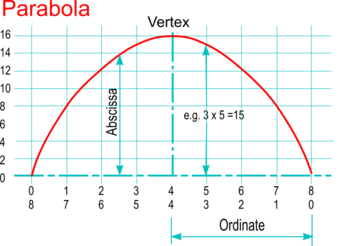
| '''Using measured [https://en.wikipedia.org/wiki/Abscissa Abscissae]''' | | '''Using measured [https://en.wikipedia.org/wiki/Abscissa Abscissae]''' | ||
| Line 38: | Line 38: | ||
* Set the height of the parabola vertex as required, and divide this into a number of equal parts up to the maximum resulting product ''(i.e. 16 in this example)'' - constructing a '''[[Scale]]''' is a convenient way of doing this. | * Set the height of the parabola vertex as required, and divide this into a number of equal parts up to the maximum resulting product ''(i.e. 16 in this example)'' - constructing a '''[[Scale]]''' is a convenient way of doing this. | ||
* Sketch a fair curve through the points ''(or use [https://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [https://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)''</span> | * Sketch a fair curve through the points ''(or use [https://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [https://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)''</span> | ||
| [[File: | | [[File:ParabolaAbscissa.png|350px|right]] | ||
|} | |} | ||
---- | ---- | ||
Revision as of 17:05, 21 February 2015
A Parabola is a Conic Section and describes the path (or trajectory) taken by a ball as it is thrown in the air.
An important characteristic of a parabola-shaped reflector is that any beam of light, sound or other energy which enters travelling parallel to its main axis is reflected through a single point called its focus. Conversely, light that originates from a point source at the focus is reflected into a parallel beam. This makes parabolic forms (i.e. parabloids) very useful for microphones and spotlight reflectors for example.
Parabolas can be drawn as the graph of y=x2 but there are other ways of drawing a parabola which exploit its various mathematical properties.
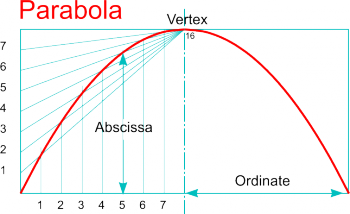
| Drawing a Parabola within a Rectangle |
|
|
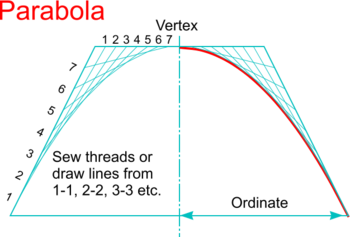
| Curve Stitching |
Note: The idea of creating curves using straight lines is put to practical use to design and build curved roofs and curve-sided towers and even bridges using straight pieces of material - see Saddle Roofs and Cooling Towers or Hyperboloid structures and The Mathematical Bridge at Cambridge for examples. |
|
| Using measured Abscissae |
|
Note: Parabolas may also be drawn by more precise methods and the position of the Focus given. Tangents and Normals may also be drawn if needed - see Conic Sections for more details.