Sundials and Gnomons: Difference between revisions

Revision as of 18:18, 12 October 2016

Introduction

Sundials' of a type may have been invented by the Ancient Egyptians and Babylonians but it was the Ancient Greeks and Romans who developed them.

At their simplest, Sundials comprise a rod (known as the Gnomon) casting the sun's shadow onto a flat plate. They are commonly mounted either horizontally or vertically but other variations also exist (e.g. on curved plates).

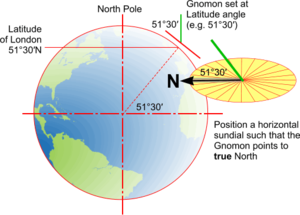
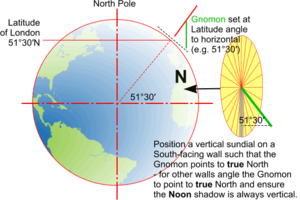
Gnomons should point to the True North and be set at an angle such that it runs parallel to the Earth's axis. This is achieved by setting it to an angle to the horizontal which is equal to the Latitude of the mounting location (e.g. 51⁰30' in London). Horizontal dials should be set level and vertical dials either placed on a South-facing wall or the Gnomon angled such that the shadow at noon is vertical.

Basic Idea

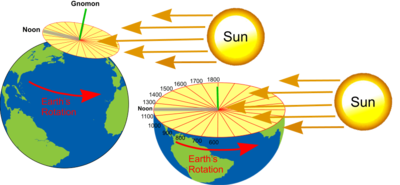
Imagine a flat circular plate at the North Pole with a ‘stick’ aligned to the Earth's vertical axis passing through it. As the Earth rotates, the Sun will cast a shadow on the plate and, since the Earth makes a complete rotation every 24 hours, the shadow will move around the plate 15⁰ for every hour (i.e. 360 degrees divided by 24).

The ‘stick’ which casts the shadow is known as the Gnomon and designs of Sundials placed on any position on the surface of the Earth should enable the Gnomon to remain parallel to the Earth's vertical axis.

Sundials where this can be achieved by having the Gnomon at right angles to the plate are known as Equatorial Sundials since the plate must be parallel to the Equator.

Horizontal Sundial

Horizontal Sundials are perhaps the most common but many are purchased with little understanding of how to make them accurate.

The shadow plate is positioned horizontal relative to its location on the Earth's surface, which means it must be Tangential to the curve of the Earth. A simple geometrical analysis will reveal that if the Gnomon is to remain parallel to the Earth's vertical axis, it must be set at an angle to the horizontal plate which is equal to the Latitude of its location.

Activity: Draw a suitably sized Circle and its vertical and horizontal Diameters. From the Circle Centre draw an angle of, say, 60⁰ for convenience and, where it intersects the Circle, draw a horizontal line to represent this line of Latitude. Draw a Tangent at the point of intersection between the line of Latitude and the Circle then show that a line draw also from this Point of Tangency but parallel to the vertical axis, must be at an angle to the Tangent equal to the Latitude.

Vertical Sundial

Activity: Search the Internet for more information on how Sundials work (e.g. The British Sundial Society).

DT Online Buyers' Guide


Brass Sundial	Large Round Slate Garden Sundial	Vertical Garden Sun Clock	Brass Armillary Sphere Sundial	Cast Iron Armillary Sundial	Sundial Compass

@@ Line 32: / Line 32: @@
-Since the shadow plate is positioned horizontal relative to its location on the Earth's surface which means it must be tangential to the curve of the Earth. A simple geometrical analysis will reveal that if the [https://en.wikipedia.org/wiki/Gnomon '''Gnomon'''] is to remain parallel to the Earth's vertical axis, it must be set at an angle to the horizontal plate which is equal to the '''[[Latitude]]''' of its location.
+The shadow plate is positioned horizontal relative to its location on the Earth's surface, which means it must be '''[[Tangents and Normals|Tangential]]''' to the curve of the Earth. A simple geometrical analysis will reveal that if the [https://en.wikipedia.org/wiki/Gnomon '''Gnomon'''] is to remain parallel to the Earth's vertical axis, it must be set at an angle to the horizontal plate which is equal to the '''[[Latitude]]''' of its location.
 ----
 <span style="color: blue">'''Activity:'''
-Draw a suitably sized circle and its vertial and horizontal diameters. From the circle centre draw an angle of, say, 60<small><sup>0</sup></small> for convenience and, where it intersects the circle, draw a horizontal line to represent this line of '''[[Latitude]]'''. Draw a tangent at the point of intersection between the line of  '''[[Latitude]]''' and the point of contact thenm show that a line draw also from this point of contact but parallel to the vertical axis must be at an angle to the tangent equal to the '''[[Latitude]]'''.
+Draw a suitably sized '''[[Circles|Circle]]''' and its vertical and horizontal '''[[Circles|Diameters]]'''. From the '''[[Circles|Circle Centre]]''' draw an angle of, say, 60<small><sup>0</sup></small> for convenience and, where it intersects the '''[[Circles|Circle]]''', draw a horizontal line to represent this line of '''[[Latitude]]'''. Draw a '''[[Tangents and Normals|Tangent]]''' at the point of intersection between the line of  '''[[Latitude]]''' and the '''[[Circles|Circle]]''' then show that a line draw also from this '''[[Tangents and Normals|Point of Tangency]]''' but parallel to the vertical axis, must be at an angle to the  '''[[Tangents and Normals|Tangent]]''' equal to the '''[[Latitude]]'''.
 </span>
 ----