Moment of Inertia: Difference between revisions
From DT Online
Moments of Inertia |
m Added Template |
||
| Line 13: | Line 13: | ||
Alternatively, and for more varied cross sections, there exists an online [http://civilengineer.webinfolist.com/str/micalc.htm '''Calculator for Moments of Inertia for plane sections''']. | Alternatively, and for more varied cross sections, there exists an online [http://civilengineer.webinfolist.com/str/micalc.htm '''Calculator for Moments of Inertia for plane sections''']. | ||
{{Terminology}} | |||
Revision as of 18:29, 18 December 2014
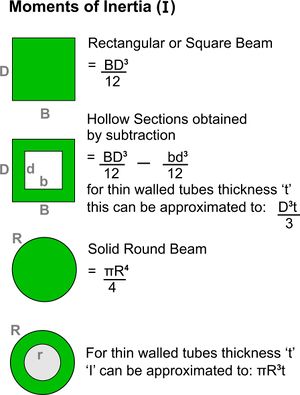
The Moment of Inertia (MI) (known more correctly as the Second Moment of Area) is used in beam bending equations. It is a measure of how resistant a body is to twisting about the Neutral Axis.
The Neutral Axis will always pass through the Centroid of a cross-section. In the case of a simple rectangular or square beams this is in the middle where the diagonals would cross and for round tubes or bars it is the circle centre.
For these concentric shapes the Moment of Inertia calculations can be simplified as shown opposite.
Other sections may be considered as being built up from these basic shapes and their Moments of Inertia about a common axis obtained. By addition of these separate Moments of Inertia and/or subtraction of the ‘MI’ for any holes or other missing areas, the ‘MI’ for the whole section can be calculated.
Alternatively, and for more varied cross sections, there exists an online Calculator for Moments of Inertia for plane sections.