Tangents and Normals

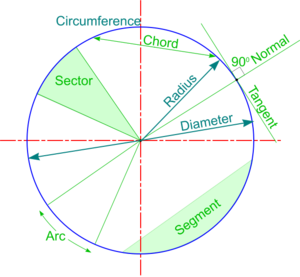
Tangents are lines just touching a given curve and its Normal is a line perpendicular to it at the point of contact (or point of Tangency).

Taking the common case of a Circle, the Normal to a Tangent from a point P on the circumference is a line joining the point to the circle centre - and the Tangent is at right angles to the Normal. This forms the basis for methods of constructing Tangents such that the Point of Tangency is given accurately.

To construct a Tangent to a Circle from a point outside its circumference:

• Join the point to the circle centre.
• Draw a semi-circle on this line as the diameter.
• The Point of Contact (or Tangency) for the Tangent is where the semi-cicle intersects the circle and its Normal joins this point to the circle centre (angle in semi-circle).

---

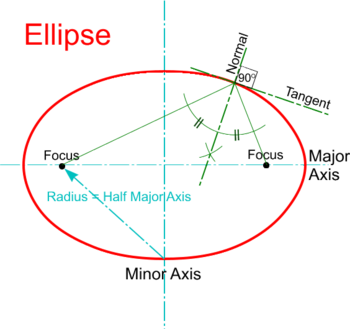
Construction of Tangents to an Ellipse

To construct a Tangent to an Ellipse from any point on the curve:

• Join the point to each of the two Foci as shown and bisect the angle found between the two lines.
• The bisector is the Normal and a Tangent may be drawn at right angles to it.

To construct a Tangent to an Ellipse from any point outside the curve:

• Strike an arc with the point as centre and radius equal to its distance from the Focus as shown.
• Strike a second arc with the second Focus as centre and radius set to equal the Major Axis.
• Join the points of intersection of the two arcs to the second Focus as shown.
• Where the two lines intersect the curve give the two Points of Tangency.
• Join the point to these Points of Tangency to produce the two possible Tangents and their Normals may be drawn at right angles to them.

---

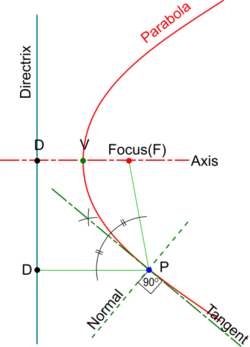
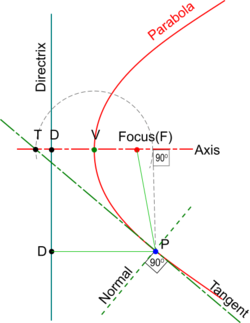
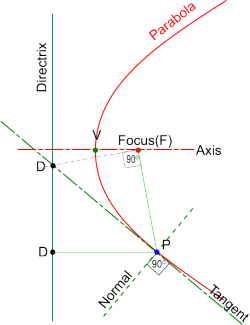
Construction of Tangents to a Parabola

---

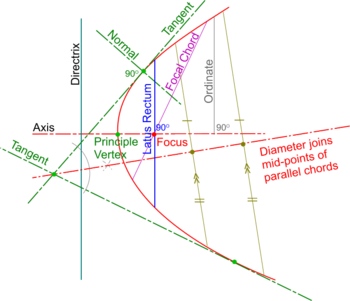
Tangents and Normals are two terms used to describe properties of all conics. Other common properties are as follows:

• A Chord is a straight line joining two points on the curve.
• A Focal Chord is a Chord which passses through the Focus
• The mid-points of parallel Chords lie in a straight line called a Diameter
• A perpendicular from a point on the Axis is called an Ordinate and if it goes straight across to the other side, it is a Double Ordinate.
• The Double Ordinate through the Focus is the Latus Rectum (translates from Latin as ‘The Right Side’).
• A Normal to any conic is at right angles to a Tangent at the Point of Contact