Nets and Developments
From DT Online
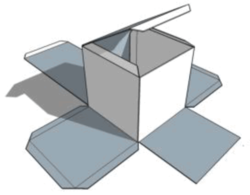
Nets and Developments are alternative names for the pattern you would need to cut out of a flat sheet to create a shape that can be folded up to form a 3 dimensional object.
Mathematicians tend to use the term ‘Net’ whereas engineers and technologists more commonly use the term ‘Development’ - perhaps because they wish to add details such as glue tabs to make sure the nets can be made in reality - but the two words are really synonymous.
| Cube |
|
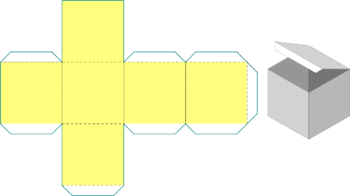 |
| Prism | ‘
Note: Polygons be constructed using the prism sides as a base - see Polygons
|
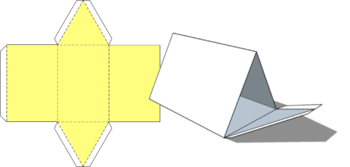 |
| Pyramid |
|
 |
| Cylinder |
|
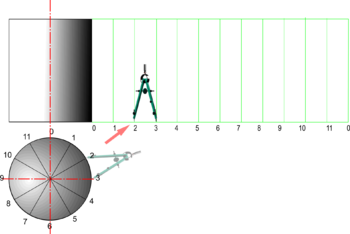 |
| Cone |
Note: Pyramids may also be drawn more easily in this way. |
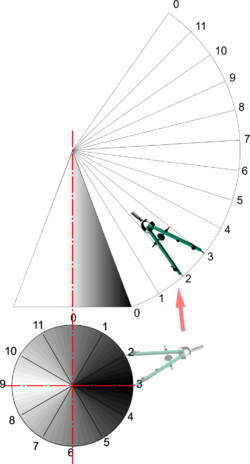 |
Note: Find some empty packaging and take it apart to see the real examples of ‘nets’ or ‘developments’ used to make them. Notice how and where they are joined so they hold together.