Description
A Scale can be used if a full-size (or true-size) drawing would be too big to fit on the paper being used or where drawing at larger than full-size is useful to show greater detail (e.g. when designing a circuit board). They can also be used to convert units of measurement (e.g. objects measured in inches drawn full-size, but in millimetres on the drawing).
Drawing at full-size is said to be drawn at a ratio of 1 : 1 (i.e. 1 unit in reality is drawn as 1 unit on paper). For a drawing to be half-size 1 unit in reality would be equal to ½ size units on paper, so would have a ratio of 1 : 2, quarter-size would be 1 : 4 and so on. The ratios are derived from a Representative Fraction which is given as:
Features and Applications
| Plain Scale
|
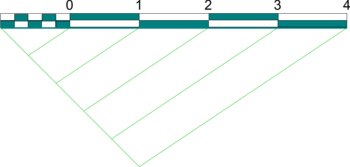
- Start by deciding how many units long the scale needs to be (e.g. the longest dimension on the drawing).
- Draw a line to represent this length to scale (e.g. half actual size)
- From one end, a second line at an angle to it.
- Step off along this second line equal divisions of any convenient size up to the number of units required.
- Join the end of the last division to the end of the first line and draw lines parallel to it through all other divisions as shown.
- Sub-divide the first scale division as required using a similar procedure and start numbering the scale from the end of this.
|
|
| Diagonal Scale
|
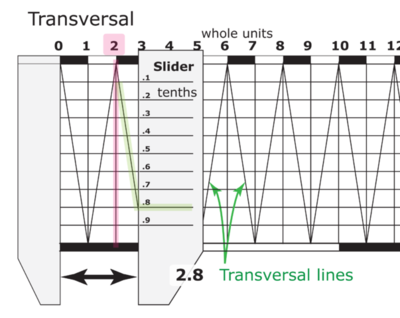
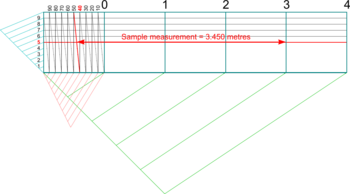
- It is not practical to create very small sub-divisions on Plain Scale, hence the need for a Diagonal Scale.
- Begin by creating a Plain Scale as above but draw a rectangle equal to the length of scale and any convenient height.
- Create the major sub-divisions as before (e.g. ¼, ½, ¾, or cm, etc.) and extend the divisions vertically.
- Divide the height of the rectangle into as many minor sub-divisions as are needed (e.g. ⅛,⅜,⅝,⅞ or mm, etc.) and draw horizontal lines through the points.
- Draw diagonals to each of the vertical rectangles created by extending the sub-divisions.
- Half way up, a diagonal would cross the rectangle at half its width and so on, thus providing the minor sub-divisions (see the example measurement shown of 3.450 metres).
|
|
Note:
There are occasions when drawing accurately to scale can provide more than a good representation, or model, of the finished product. Scale drawings can be measured from and used to transfer sizes of a complex shape on to a large sheet of material for example, but in general and with the advent of CAD, measuring off an Engineering Drawing is not as common as it once was - and has never been satisfactory for really accurate work.