Circles
From DT Online
Description
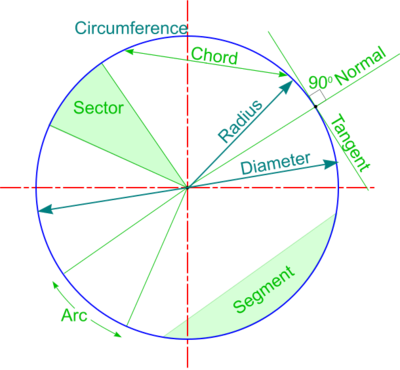
Circles are very familiar but have associated with them terminology, properties and characteristics with which all involved with design and technology should understand.
A particular property of a circle is that its radius can be stepped off around its circumference exactly 6 times. In effect, this constructs 6 equi-lateral triangles, the interior angles of which are all 600, and the sum of all angles at the centre of any polygon must equal 3600.
The sides of these equi-lateral triangles become chords of the circle and should not be confused with the length of an arc, which is longer. Lengths of arcs can be found by dividing the circumference by the number of sides. The circumference is calculated as 2πr or πD (π is a constant obtained by dividing circumference by diameter - i.e. approximately 3.142)".
Constructions
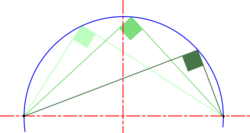
| Angle in a Semi-Circle |
Note: If angles are drawn in each half of the circle the result would be a particular case of cyclic quadlitaleral which makes it easier to see the more general case that the sum of opposite internal angles of any cyclic quadlitaleral is always equal to 1800. |
|
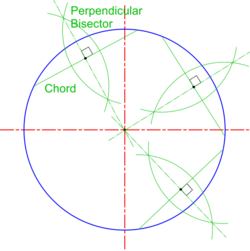
| Bisecting Chords |
|
|
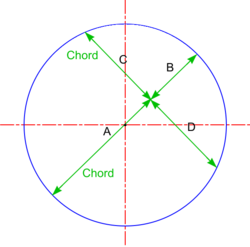
| Intersecting Chords Theorem |
Note: This is a particular case of the Intersecting Chords Theorem which states that the relationship (A x B = C x D) is true for any two intersecting chords, whether or not one of them is a diameter
|
|
| Tangent from a Point Outside a Circle |
Note: This concept is the basis of the design of Centre Squares ( or Centre Finders) |