Cycloid

Description

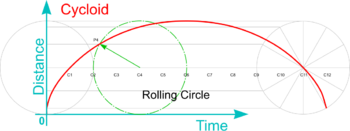
An Cycloid is the path traced by a point on the circumference of a circle as it rolls without slipping along a straight line. The curve has been used to design gear teeth and has sometimes been used by architects to design the shape of a curved roof. The term ‘cycloid’ is used also to describe the shape of some fish scales.

A line produced by a point following a set of rules in this way is known as the locus of a point (plural is loci).

Constructions

Drawing a Cycloid

Draw a starting circle and divide into equal segments (say, 12) Draw a horizontal line for the circle to roll along, of length equal to the circle circumference, and divide this into the same number of equal parts. (Constructions used to create Scales are convenient ways of doing this). Project lines parallel to the base line at heights representing the heights reached by the points on the circle as it rolls round. Start at 0 then describe a circle from the second centre position on to the first line above the baseline, which shows the height the point now reaches. Repeat this procedure for each progressive centre position as shown. Sketch a fair curve through the points (or use French Curves or a flexible strip for example).

---

Note: The cycloid is a special case of Trochoid in which the point traced is on the circumference of the rolling circle. Using a similar technique, Superior and Inferior Trochoids can also be generated by plotting points either outside (as the tip of a paddle wheel as a boat is propelled by it) or inside the rolling circle (as if marked on a rolling disc for example) . Also, by similar trechniques, the base line can be replaced by a base circle and the rolling circle rolled around either the inside or the outside of it to generate Hypocycloids or Epicycloids - as used in Epicyclic Gearing for example ,

---

DT Online Buyers' Guide

Helix Oxford Maths Set	Linex Student Saver Bundle	Helix Precision Plus Drawing Set	Primary Shape Template Set	Linex Circle Template	Helix National Curriculum Drawing Set	Helix 3 Piece Stencil Set	Linex Universal Architects Template	French Curve Transparent Template	T-Square