Fibonacci Series
From DT Online
Description
In the year 1202, and Italian mathematician, Leonardo of Pisa (known as Fibonacci) introduced a sequence of numbers, which has since been applied to topics as diverse as art, architecture, natural forms and population growth. The Fibonacci Series is a sequence of numbers in which the next number is found by adding up the two numbers before it.
The sequence is of interest to designers because it would appear to have some relationship with proportions found in nature and, perhaps as a result of this, our own preferences.
Activity: Ask your friends to divide a line in two such that there is a pleasing relationship between the two parts. Most people may find that dividing the line into two equal parts lacks interest, and making one part much bigger than the other unbalanced, so they will opt for a division somewhat off-centre - but not too much. If this is done with a number of people, a preference for the line to be divided roughly into one third and two thirds will probably emerge (i.e. a ratio similar to adjacent numbers in the series).
This activity is described with others in Kurt Rowland's book 'The Shapes We Need' (from the excellent 'Looking and Seeing'
series).
It is common practice when composing a photograph or painting a picture to follow this Rule of Thirds such that the main focus or point of interest is approximately one third along, up or down the composition and not in the centre.
Fibonacci Numbers are also found throughout the natural world. Counting the petals of flowers and seed heads, measuring the distance between tree branches or looking at the proportions of animals have all been claimed to reflect numbers on the Fibonacci Series.
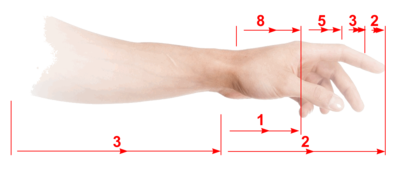
Activity:
Measure the distances between the various joints on your fingers and arm as shown. Ask your friends to do the same, make a list of everyone's results and find the average for each measurement (you may wish to use a Spreadsheet for this) and 'round' the results to the nearest whole number. Do the results match the proportions shown?
Calculating the proportions or Ratios is key to seeing any similarities. For the line division activity, divide the length of the large part by the small part and, from the table of arm measurements, take two adjacent or connected measurements (e.g. forearm and hand) and divide the larger by the smaller. It is likely that this will result in numbers approaching 1.6.
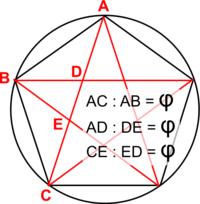
This natural proportion is known as the Golden Ratio which is a special number approximately equal to 1.618 and given the Greek letter Φ (phi). What we now know as the Golden Ratio or Golden Section has been studied for thousands of years, starting with the Ancient Greeks and first described by Euclid. The proportion is alleged to be in evidence in Greek architecture and the Greeks used the Pentagon, which has a number of Φ (phi) relationships, as a holy symbol.
It was discovered that the Golden Ratio can be estimated by taking any two successive numbers from the Fibonacci Series and dividing the larger one by the one below it:
e.g.
. . . and so on - note that the further we go along the Fibonacci Series the closer we get to 1.618.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| A3 Cartridge Paper |
A3 Layout Pad |
A3 Marker Pad |
A3 Coloured Pad |
A3 Tracing Paper |
A3 Graph Pad |
A3 Drawing Board |
Drawing and Sketching Pencil Art Set |
Coloured Pencil Set |
A3 Light Box |