Description
An Spiral is a line traced by a point which starts at a centre then gets progressively further away as it travels around it. There are many different ways of drawing spirals each with different mathematical properties.
A vynil record groove is a good example of a spiral (but the early, antique phonograph cylinders follow a helix. Spiral staircases are also in fact helixes and not really spirals at all (!) but 3D spirals do exist, examples of which include the springs commonly used as a battery contact in torches and some snail shells).
Constructions
| Drawing a Common Spiral
|
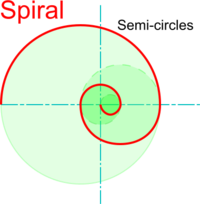
- It is possible to draw a spiral-like curve using only semi-circles. This is not a true spiral but is often sufficient for illustration purposes.
- Start by drawing a line of any length then describe a small semi-circle somewhere near the centre.
- Use the diameter of the first semi-circle as the radius for a second sem-circle described from one end of the first one.
- Draw a third semi-circle from one end of the second with its radius set to the diamater of the second semi-circle.
- Repeat this procedure until you have enough turns or a large enough spiral for your purposes.
|
|
| Constructing an Archimedean Spiral
|
- Named after the famous ancient Greek mathematician, Archimedes, this spiral is: the path traced by a point as it moves away with constant linear velocity, from the centre of a circle which is rotating with constant angular velocity.
- A line produced by a point following a set of rules in this way is known as the locus of a point (plural is loci).
- Start by drawing a number of equi-spaced concentric circles (say, 12) and divide one complete revolution into the same number of equal parts.
- The intersection between the circle from point 1 on the line and radial line 1 provide point 1 on the spiral.
- Plot all other points in this way and draw a smooth curve through them (or use French Curves or a flexible strip for example)
|
|
| Constructing Spiral using Golden Rectangles
|
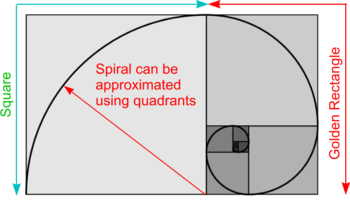
- A Golden Rectangle is one in which the sides are in a particular proportion known as the Golden Ratio or Golden Section. A good way of approximating this ratio is to use the Fibonacci series which is created by making each number the sum of the two before it - i.e. 1,1,2,3,5,8,13,21, etc. The further along the sequence you go: the nearer you get to the Golden Ratio.
- It is a property of a Golden Rectangle that when a square is added to its longest side, another, larger, Golden Rectangle is created.
- Start by drawing a square of any size (but for ease, make its length of side divisable by a number on the Fibonacci series - say,5)
- Draw a rectangle where one side is the side of the square and the shorter side has a length proportional to the number below it on the Fibonacci series (say, 3).
- Draw a large square from the side of the first square plus the shorter side of the rectangle (length now, say, 8) and repeat the process.
- An approximate spiral can be created by drawing quarter circles, or quadrants, in each of the squares as shown.
|
|