Spiral: Difference between revisions
From DT Online
(Added category links) |
(Changed Images) |
||
| Line 17: | Line 17: | ||
</span> | </span> | ||
| [[File: | | [[File:CommonSpiralConstruction.png|200px|right]] | ||
|- | |- | ||
| '''Constructing an Archimedean Spiral''' | | '''Constructing an Archimedean Spiral''' | ||
| Line 26: | Line 26: | ||
* The intersection between the circle from point 1 on the line and radial line 1 provide point 1 on the spiral. | * The intersection between the circle from point 1 on the line and radial line 1 provide point 1 on the spiral. | ||
* Plot all other points in this way and draw a smooth curve through them ''(or use [https://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [https://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)''</span> | * Plot all other points in this way and draw a smooth curve through them ''(or use [https://en.wikipedia.org/wiki/French_curve '''French Curves'''] or a [https://en.wikipedia.org/wiki/Flat_spline '''flexible strip'''] for example)''</span> | ||
| [[File: | | [[File:ArchimedeanSpiralConstruction.png|250px|right]] | ||
|- | |- | ||
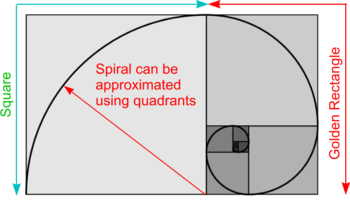
| '''Constructing Spiral using Golden Rectangles''' | | '''Constructing Spiral using Golden Rectangles''' | ||
| Line 36: | Line 36: | ||
* Draw a large square from the side of the first square plus the shorter side of the rectangle ''(length now, say, 8)'' and repeat the process. | * Draw a large square from the side of the first square plus the shorter side of the rectangle ''(length now, say, 8)'' and repeat the process. | ||
* An approximate spiral can be created by drawing quarter circles, or quadrants, in each of the square as shown. | * An approximate spiral can be created by drawing quarter circles, or quadrants, in each of the square as shown. | ||
| [[File: | | [[File:GoldenSpiralConstruction.png|350px|right]] | ||
|} | |} | ||
Revision as of 17:14, 21 February 2015
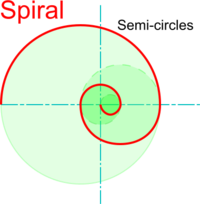
An Spiral is a line traced by a point which starts at a centre which it gets progressively further away from as it travels around it. There are many different ways of drawing spirals each with different mathematical properties.
A vynil record groove is a good example of a spiral (but the early, antique phonograph cylinders follow a helix. Spiral staircases are also in fact helixes and not really spirals at all (!) but 3D spirals do exist, examples of which include the springs commonly used as a battery contact in torches and some snail shells .
| Drawing a Common Spiral |
|
|
| Constructing an Archimedean Spiral |
|
|
| Constructing Spiral using Golden Rectangles |
|