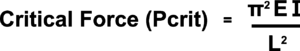Buckling: Difference between revisions
From DT Online
(Added Template) |
m (Adde book link) |
||
| Line 8: | Line 8: | ||
::::::::::[[File:EulersBucklingEquation.png|300px|bottom]] | ::::::::::[[File:EulersBucklingEquation.png|300px|bottom]] | ||
See - [https://www.amazon.co.uk/gp/product/0140135979/ref=as_li_qf_sp_asin_il_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=0140135979&linkCode=as2&tag=dton06-21 ''''The New Science of Strong Materials: Or Why You Don't Fall Through the Floor' by J.E.Gordon'''] | |||
Revision as of 10:06, 14 November 2016
Description
A Structural Member in Compression (i.e. a Strut) is more likely to buckle first when subjected to pressure - assuming the Strut is made of a sensible material and not something so brittle it is likely to explode under pressure(!)
See - 'The New Science of Strong Materials: Or Why You Don't Fall Through the Floor' by J.E.Gordon
Features and Applications
The point at which a strut might buckle can be assessed using a simplified form of Euler's Buckling Equation as follows:
Where:
- Pcrit = the Critical Force at which the strut will start to buckle.
- E = the Young's Modulus of the material (obtainable from tables or by experiment).
- Capital I = the Moment of Inertia about the Neutral Axis (for a rectangular beam this is its breadth times the depth cubed divided by 12).
- L = the length of the Strut (this is taken as the total length if the strut is assumed to be pin-jointed at each end but would vary with other fixing methods - see Euler's Buckling Equation)
|
Click top left to enlarge |