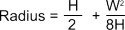Circles: Difference between revisions
From DT Online
Adding examples and Category Links |
Added Template |
||
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:CircleParts.png| | [[File:CircleParts.png|400px|right]] | ||
__TOC__ | |||
=====Description===== | |||
[https://en.wikipedia.org/wiki/Circle '''Circles'''] are very familiar but have associated with them terminology, properties and characteristics with which all involved with '''[[Design and Technology|design and technology]]''' should understand. | [https://en.wikipedia.org/wiki/Circle '''Circles'''] are very familiar but have associated with them terminology, properties and characteristics with which all involved with '''[[Design and Technology|design and technology]]''' should understand. | ||
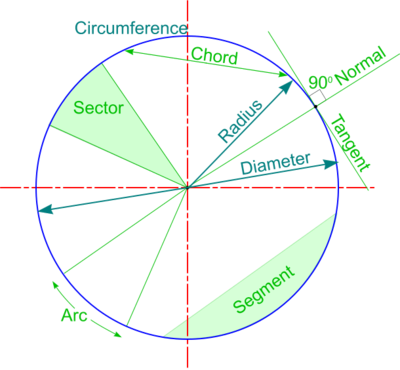
A particular property of a circle is that its '''radius''' can be stepped off around its '''circumference''' exactly 6 times. | |||
A particular property of a circle is that its '''radius''' can be stepped off around its '''circumference''' exactly 6 times. In effect, this constructs 6 equi-lateral triangles, the interior angles of which are all 60<sup>0</sup>, and the sum of all angles at the centre of <u>any</u> '''[[Polygons|polygon]]''' must equal 360<sup>0</sup>. | |||
The sides of these equi-lateral triangles become '''chords''' of the circle and should not be confused with the length of an '''arc''', which is longer. Lengths of arcs can be found by dividing the circumference by the number of sides. The circumference is calculated as 2πr or πD ''([https://en.wikipedia.org/wiki/Pi '''π'''] is a constant obtained by dividing circumference by diameter - i.e. approximately 3.142)". | The sides of these equi-lateral triangles become '''chords''' of the circle and should not be confused with the length of an '''arc''', which is longer. Lengths of arcs can be found by dividing the circumference by the number of sides. The circumference is calculated as 2πr or πD ''([https://en.wikipedia.org/wiki/Pi '''π'''] is a constant obtained by dividing circumference by diameter - i.e. approximately 3.142)". | ||
=====Constructions===== | |||
{| cellpadding="5" | {| cellpadding="5" | ||
|- | |- | ||
| '''Angle in a Semi-Circle''' | | '''Angle in a Semi-Circle''' | ||
| <span style="color:#B00000"> | | <span style="color:#B00000"> | ||
* <u>Any</u> angle drawn | * <u>Any</u> angle drawn by connecting each end of a semi-circle diameter to point on its circumference is a right angle. | ||
---- | ---- | ||
<span style="color: green">'''Note:''' | <span style="color: green">'''Note:''' | ||
| Line 24: | Line 32: | ||
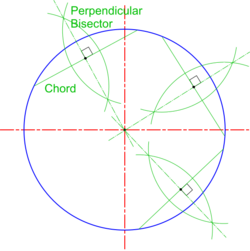
* The '''[[Basic Constructions|perpendicular bisectors]]''' of <u>any</u> two chords to a circle will intersect at the centre of that circle | * The '''[[Basic Constructions|perpendicular bisectors]]''' of <u>any</u> two chords to a circle will intersect at the centre of that circle | ||
* In practice, a 3rd chord is also bisected as shown to serve as an accuracy check when finding the circle centre. | * In practice, a 3rd chord is also bisected as shown to serve as an accuracy check when finding the circle centre. | ||
</span> | </span> | ||
| [[File:IntersectingChords.png|250px|right]] | | [[File:IntersectingChords.png|250px|right]] | ||
| Line 34: | Line 37: | ||
| '''Intersecting Chords Theorem''' | | '''Intersecting Chords Theorem''' | ||
| <span style="color:#B00000"> | | <span style="color:#B00000"> | ||
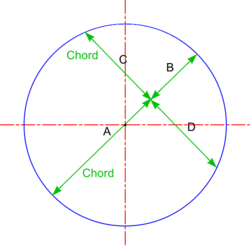
* Looking at one of the chords and its bisector above, | * Looking at one of the chords and its bisector above, '''[[Intersecting Chords|it can be proved]]''' that '''A x B = C x D'''.<div style="clear: both;"></div> | ||
* It can be derived from this that | * It can be derived from this that '''[[Intersecting Chords|finding the centre of an arch]]''' doorway or window for example can be found by the formula: | ||
[[File:ArcRadius.png|125px|right]] | |||
: Where: '''W''' is the length of the chord defining the base of the arc and '''H''' is the height measured at the midpoint of the arc's base. | : Where: '''W''' is the length of the chord defining the base of the arc and '''H''' is the height measured at the midpoint of the arc's base. | ||
---- | |||
<span style="color: green">'''Note:''' | |||
This is a particular case of the '''[[Intersecting Chords|Intersecting Chords Theorem]]''' which states that the relationship ''(A x B = C x D)'' is true for <u> any</u> two intersecting chords, whether or not one of them is a diameter | |||
</span> | |||
---- | |||
</span> | |||
| [[File:ChordsTheorem.png|250px|right]] | | [[File:ChordsTheorem.png|250px|right]] | ||
|- | |- | ||
| Line 43: | Line 52: | ||
| <span style="color:#B00000"> | | <span style="color:#B00000"> | ||
* For most practical purposes, especially with large-scale work, it can be satisfactory simply to draw a line touching a circle as the '''tangent''' | * For most practical purposes, especially with large-scale work, it can be satisfactory simply to draw a line touching a circle as the '''tangent''' | ||
* There may be occasions however when it is important to know exactly where the tangent touches the circle circumference ''(i.e. the Point of Tangency | * There may be occasions however when it is important to know exactly where the tangent touches the circle circumference ''(i.e. the Point of Tangency)'' | ||
* For points on the circumference, the tangent is simply drawn as a line at right angles to a line joining the point to the circle centre ''(i.e. the Normal)''. | * For points on the circumference, the tangent is simply drawn as a line at right angles to a line joining the point to the circle centre ''(i.e. the Normal)''. | ||
* Points outside the circumference exploit the property of ''Angles in a Semi-Circle'' as described above. | * Points outside the circumference exploit the property of ''Angles in a Semi-Circle'' as described above. | ||
* | * For points outside the circle, join the point to the circle centre and construct a semi-circle on this line. | ||
* Where the semi-circle cuts the circumference provides the ''Point of Tangency'' to which may be drawn both the ''Normal'' and ''Tangent'' required. | * Where the semi-circle cuts the circumference provides the ''Point of Tangency'' to which may be drawn both the ''Normal'' and ''Tangent'' required. | ||
---- | |||
<span style="color: green">'''Note:''' | |||
This concept is the basis of the design of '''[[Squares|Centre Squares]]''' ''( or Centre Finders)'' | |||
</span> | |||
----</span> | |||
| [[File:TangentPointCircle.png|250px|right]] | | [[File:TangentPointCircle.png|250px|right]] | ||
|} | |} | ||
{{Drawing Instruments Buyers Guide}} | |||
[[Category:Secondary]] | [[Category:Secondary]] | ||
[[Category:Geometry]] | [[Category:Geometry]] | ||
Latest revision as of 18:53, 2 June 2016
Description
Circles are very familiar but have associated with them terminology, properties and characteristics with which all involved with design and technology should understand.
A particular property of a circle is that its radius can be stepped off around its circumference exactly 6 times. In effect, this constructs 6 equi-lateral triangles, the interior angles of which are all 600, and the sum of all angles at the centre of any polygon must equal 3600.
The sides of these equi-lateral triangles become chords of the circle and should not be confused with the length of an arc, which is longer. Lengths of arcs can be found by dividing the circumference by the number of sides. The circumference is calculated as 2πr or πD (π is a constant obtained by dividing circumference by diameter - i.e. approximately 3.142)".
Constructions
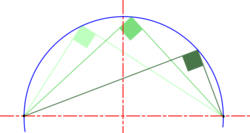
| Angle in a Semi-Circle |
Note: If angles are drawn in each half of the circle the result would be a particular case of cyclic quadlitaleral which makes it easier to see the more general case that the sum of opposite internal angles of any cyclic quadlitaleral is always equal to 1800. |
 |
| Bisecting Chords |
|
 |
| Intersecting Chords Theorem |
Note: This is a particular case of the Intersecting Chords Theorem which states that the relationship (A x B = C x D) is true for any two intersecting chords, whether or not one of them is a diameter
|
 |
| Tangent from a Point Outside a Circle |
Note: This concept is the basis of the design of Centre Squares ( or Centre Finders) |
 |