Intersecting Chords
From DT Online
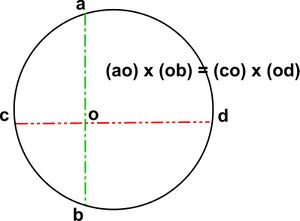
This theorem relates to a characteristic of a cyclic quadlitateral, the diagonals of which are two intersecting chords of the circumscribing circle.
The Intersecting Chords Theorem states that the relationship (ao x ob = co x od) is true for any two intersecting chords, whether or not one of them is a diameter.
| Measuring Beam Deflections |
The theorem can be useful when measuring the radius of bending of a deflected beam if one of the chords is taken to be the length of the beam e.g.
Bending Radius (R) can be calculated as follows:
(see Structures: Or Why Things Don't Fall Down by J.E.Gordon |
 |