Bending Moment: Difference between revisions
From DT Online
Created article |
Added Template |
||
| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Bending Moment Diagram.png| | [[File:Bending Moment Diagram.png|300px|right]] | ||
__TOC__ | |||
=====Description===== | |||
A '''[[Moment of Force|Moment]]''' is calculated by multiplying a '''Force''' ''(in '''[[newton|newtons]]''')'' by its distance from a fixed point or pivot ''(in '''metres''')''. | A '''[[Moment of Force|Moment]]''' is calculated by multiplying a '''Force''' ''(in '''[[newton|newtons]]''')'' by its distance from a fixed point or pivot ''(in '''metres''')''. | ||
| Line 6: | Line 11: | ||
The [http://en.wikipedia.org/wiki/Bending_Moment '''Bending Moment''' '''''(B.M.)'''''] for a '''[[Simply Supported Beam]]''' about either of the '''[[Reactions]]''' ''(or supports)'' from any point a distance ''''x'''' from them can be expressed as '''Wx / 2'''. If the load is in the centre of the beam, as shown, the maximum '''B.M.''' can be seen to be equal to: '''Load x Span divided by 4''' | =====Features and Applications===== | ||
The [http://en.wikipedia.org/wiki/Bending_Moment '''Bending Moment''' '''''(B.M.)'''''] for a '''[[Simply Supported Beam]]''' about either of the '''[[Reactions (structures)|Reactions]]''' ''(or supports)'' from any point a distance ''''x'''' from them can be expressed as '''Wx / 2'''. If the load is in the centre of the beam, as shown, the maximum '''B.M.''' can be seen to be equal to: '''Load x Span divided by 4''' | |||
| Line 21: | Line 28: | ||
Self-weight can be assumed to be the same as a single point load acting on the centre of a beam or the cantilever. In the case of the cantilever example shown, self-weight would be acting therefore a quarter of the way along the beam - or '''Length = L/4''' and the maximum '''B.M.= W/2 x L/4 = WL/8''' | Self-weight can be assumed to be the same as a single point load acting on the centre of a beam or the cantilever. In the case of the cantilever example shown, self-weight would be acting therefore a quarter of the way along the beam - or '''Length = L/4''' and the maximum '''B.M.= W/2 x L/4 = WL/8''' | ||
<div style="clear: both;"></div> | |||
{{Construction Kits Buyers Guide}} | |||
[[Category:Terminology]] | [[Category:Terminology]] | ||
Latest revision as of 20:23, 3 September 2016
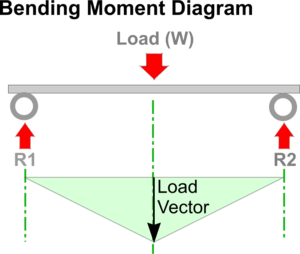
Description
A Moment is calculated by multiplying a Force (in newtons) by its distance from a fixed point or pivot (in metres).
A value for the Maximum Bending Moment (B.M.) is needed when calculating the strength of a beam using the Simple Bending Equation for example.
Features and Applications
The Bending Moment (B.M.) for a Simply Supported Beam about either of the Reactions (or supports) from any point a distance 'x' from them can be expressed as Wx / 2. If the load is in the centre of the beam, as shown, the maximum B.M. can be seen to be equal to: Load x Span divided by 4
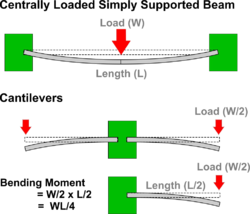
To understand why this is so, imagine the beam to be cut into two then the two halves placed back to back to create two cantilevers each supporting half of the load - and each cantilever will be half the length of the beam of course.
It is clear that standing on the end of a diving board makes it bend the most and this is where to find the Maximum Bending Moment. Moments are given as Force x Distance and in this case, the force is that exerted by the half of the original beam load (W/2) x half the length of the beam (L/2). This can be expressed as Load x Span divided by 4 as shown
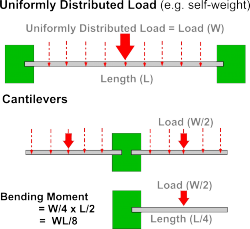
In the case of a beam bearing a uniformly distributed load (such as the beam's self-weight) the Maximum Bending Moment (B.M.) is equal to Load x Span divided by 8 (which can also be written as half the load x a quarter of the span)
Self-weight can be assumed to be the same as a single point load acting on the centre of a beam or the cantilever. In the case of the cantilever example shown, self-weight would be acting therefore a quarter of the way along the beam - or Length = L/4 and the maximum B.M.= W/2 x L/4 = WL/8
|
Click top left to enlarge |








