Gear Nomenclature: Difference between revisions
From DT Online
mNo edit summary |
mNo edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:GearNomenclature.png|500px|right]] | [[File:GearNomenclature.png|500px|right]] | ||
__TOC__ | |||
=====Description===== | |||
Two smooth surfaced discs can be imagined to be in contact with each other such that one drives the other by friction. It is clear that when a load of any significance is applied the discs would slip. To avoid this problem, the surfaces are modified to have teeth which engage with each other. This is the basis of [https://en.wikipedia.org/wiki/Gear '''Gear'''] design. | Two smooth surfaced discs can be imagined to be in contact with each other such that one drives the other by friction. It is clear that when a load of any significance is applied the discs would slip. To avoid this problem, the surfaces are modified to have teeth which engage with each other. This is the basis of [https://en.wikipedia.org/wiki/Gear '''Gear'''] design. | ||
=====Terms===== | |||
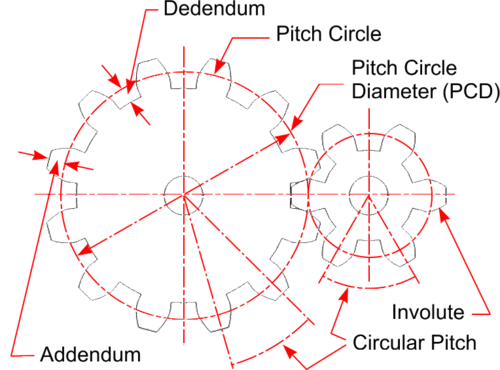
* Cicles representing the two imaginery discs are known as '''Pitch Circles''' and their diameters are the '''Pitch Circle Diameters''' or '''PCDs''' ''(aka Reference Diameters)''. | * Cicles representing the two imaginery discs are known as '''Pitch Circles''' and their diameters are the '''Pitch Circle Diameters''' or '''PCDs''' ''(aka Reference Diameters)''. | ||
* Gear teeth are created by: | * Gear teeth are created by: | ||
| Line 7: | Line 16: | ||
* Gear teeth will only '''Mesh''' if they are the same size in that the distances around the circumferences of their '''PCDs''' must be equal. This distance is known as the '''Circular Pitch'''. | * Gear teeth will only '''Mesh''' if they are the same size in that the distances around the circumferences of their '''PCDs''' must be equal. This distance is known as the '''Circular Pitch'''. | ||
* The size of gear teeth is more easily calculated by dividing the diameter of the '''Pitch Circle''' by the number of gear teeth. This is known as the '''Modulus''' or '''Module (m)''' and must be the same for any meshing gears. | * The size of gear teeth is more easily calculated by dividing the diameter of the '''Pitch Circle''' by the number of gear teeth. This is known as the '''Modulus''' or '''Module (m)''' and must be the same for any meshing gears. | ||
* The diameters of the '''Pitch Circles''' can be used when calculating '''[[Velocity Ratio]]''' and is given as: '''Driver PCD ÷ Driven PCD'''. | |||
* The curve of the gear teeth is an '''[[Involute]]''', chosen to provide a true rolling contact without slipping as the gears engage. | * The curve of the gear teeth is an '''[[Involute]]''', chosen to provide a true rolling contact without slipping as the gears engage. | ||
More details including descriptions of other aspects of gear design can be obtained by [https://en.wikipedia.org/wiki/Gear '''further reading ''']. | More details including descriptions of other aspects of gear design can be obtained by [https://en.wikipedia.org/wiki/Gear '''further reading ''']. | ||
{{Gears Buyers Guide}} | |||
[[Category:Gears]] | [[Category:Gears]] | ||
[[Category:Terminology]] | [[Category:Terminology]] | ||
Latest revision as of 19:31, 3 September 2016
Description
Two smooth surfaced discs can be imagined to be in contact with each other such that one drives the other by friction. It is clear that when a load of any significance is applied the discs would slip. To avoid this problem, the surfaces are modified to have teeth which engage with each other. This is the basis of Gear design.
Terms
- Cicles representing the two imaginery discs are known as Pitch Circles and their diameters are the Pitch Circle Diameters or PCDs (aka Reference Diameters).
- Gear teeth are created by:
- (i) cutting into the Pitch Circles - the depth of cut is known as the Dedendum and
- (ii) adding material on top of the Pitch Circles - the distance between the PCD and the outer diameter of the gear is known as the Addendum.
- Gear teeth will only Mesh if they are the same size in that the distances around the circumferences of their PCDs must be equal. This distance is known as the Circular Pitch.
- The size of gear teeth is more easily calculated by dividing the diameter of the Pitch Circle by the number of gear teeth. This is known as the Modulus or Module (m) and must be the same for any meshing gears.
- The diameters of the Pitch Circles can be used when calculating Velocity Ratio and is given as: Driver PCD ÷ Driven PCD.
- The curve of the gear teeth is an Involute, chosen to provide a true rolling contact without slipping as the gears engage.
More details including descriptions of other aspects of gear design can be obtained by further reading .
|
Click top left to enlarge |