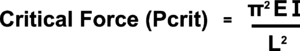Buckling

Description

A Structural Member in Compression (i.e. a Strut) is more likely to buckle first when subjected to pressure - assuming the Strut is made of a sensible material and not something so brittle it is likely to explode under pressure(!)

See - 'The New Science of Strong Materials: Or Why You Don't Fall Through the Floor' by J.E.Gordon

Features and Applications

The point at which a strut might buckle can be assessed using a simplified form of Euler's Buckling Equation as follows:

Where:

• Pcrit = the Critical Force at which the strut will start to buckle.
• E = the Young's Modulus of the material (obtainable from tables or by experiment).
• Capital I = the Moment of Inertia about the Neutral Axis (for a rectangular beam this is its breadth times the depth cubed divided by 12).
• L = the length of the Strut (this is taken as the total length if the strut is assumed to be pin-jointed at each end but would vary with other fixing methods - see Euler's Buckling Equation)

DT Online Buyers' Guide

Simple Frames and Linkages can be explored using Construction Kits such as those listed below. More varied models can be constructed using the materials listed at Truss Bridge Models or Stripwood Technology Materials and tools described in Stripwood Technology Tools.

Load video YouTube YouTube might collect personal data. Privacy Policy ContinueDismiss Click top left to enlarge

Viga Wooden Construction Set	Straws and Connectors	Construction Engineering Blocks	K'Nex Education Group Set	Engino STEM Construction Set	Lego Duplo Tech Machines Set	Lego Education Core Set	Meccano Easy Construction Box	Fischertechnik Universal Building Kit