Intersecting Chords: Difference between revisions
From DT Online
(Intersecting Chords Theorem) |
(Added chords diagram) |
||
| Line 3: | Line 3: | ||
It can be useful when measuring the radius of bending of a deflected beam, for example, if one of the chords is taken to be the length of the beam | It can be useful when measuring the radius of bending of a deflected beam, for example, if one of the chords is taken to be the length of the beam | ||
[[File:DeflectedBeamChords.jpg|400px|right]] | |||
e.g. | e.g. | ||
# set up a strip of material as a simple beam | |||
# note the distance between supports '''''(cd)''''' | |||
# apply a central load to make it bend - or '''''[[Beam Deflection|‘deflect’(Δ)]]''''' - therefore '''co = od = ½cd''' | |||
# measure the deflection '''''(ob)''''' | |||
Bending Radius (R) can be calculated as follows: | |||
* ao x ob = co x od | |||
* (2R-Δ) x Δ = ½cd x ½cd | |||
* but, for small deflections, Δ<sup>2</sup> will be negligible | |||
* so R = cd<sup>2</sup> ÷ 8 x Δ | |||
''(see ‘Structures’ by J.E.Gordon ISBN 0 14 02.1961 7)'' | |||
Revision as of 10:33, 7 November 2014
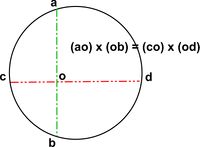
This theorem relates to a characteristic of a cyclic quadlitateral, the diagonals of which are two intersecting chords of the circumscribing circle.
It can be useful when measuring the radius of bending of a deflected beam, for example, if one of the chords is taken to be the length of the beam
e.g.
- set up a strip of material as a simple beam
- note the distance between supports (cd)
- apply a central load to make it bend - or ‘deflect’(Δ) - therefore co = od = ½cd
- measure the deflection (ob)
Bending Radius (R) can be calculated as follows:
- ao x ob = co x od
- (2R-Δ) x Δ = ½cd x ½cd
- but, for small deflections, Δ2 will be negligible
- so R = cd2 ÷ 8 x Δ
(see ‘Structures’ by J.E.Gordon ISBN 0 14 02.1961 7)