Corbusier's Modulor: Difference between revisions
From DT Online
(Added Template) |
mNo edit summary |
||
| Line 2: | Line 2: | ||
=====Description===== | |||
The French Architect, [https://en.wikipedia.org/wiki/Le_Corbusier '''Le Corbusier'''] devised in the mid-20th century, a system of proportions and measurements he called the [https://en.wikipedia.org/wiki/Modulor '''Modulor''']. | The French Architect, [https://en.wikipedia.org/wiki/Le_Corbusier '''Le Corbusier'''] devised in the mid-20th century, a system of proportions and measurements he called the [https://en.wikipedia.org/wiki/Modulor '''Modulor''']. | ||
Latest revision as of 18:07, 5 July 2016
Description
The French Architect, Le Corbusier devised in the mid-20th century, a system of proportions and measurements he called the Modulor.
The Modulor divides the height of the average man in Golden Ratio proportions to produce a scale of measurements as shown. Taking the initial average used of 1829mm the first division would make the longer of the two parts 1130mm and this corresponds to the height of the navel. It is interesting to note that Leonardo da Vinci also used the human navel, as the centre of his circle, when he constructed the Vitruvian Man as part of his work to devise a scale of measurements based on human proportions.
Le Corbusier continued to divide and sub-divide to produce two scales: one with a standing figure (Column A) and one standing with an arm extended upwards (Column B). The two columns are Fibonacci Series and each value on the scale is the sum of the two values preceding it.
Proportions based on the Golden Ratio are visually pleasing and so adding human dimensions produces a system with which we design products, furniture and even buildings, which not only look harmonious but also fit the human frame's Anthropometrics. The result is furniture which is a comfortable height for sitting or eating at for example.
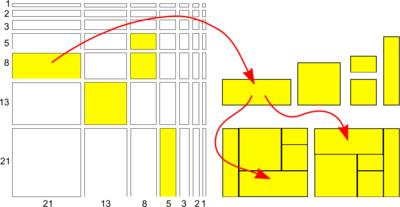
A matrix can be constructed using all the measurements of the Modulor to create a series of rectangles. Different rectangles taken from it are easily fitted together and/or easily sub-divided into a number of smaller panels. This is because, being a Fibonacci Series, each measurement on the scale is the sum of the two before it. A similar matrix can be created using Fibonacci Numbers as shown.
Such grids are very useful when shapes have to be sub-divided to design storage units or position windows in buildings for example.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| A3 Cartridge Paper |
A3 Layout Pad |
A3 Marker Pad |
A3 Coloured Pad |
A3 Tracing Paper |
A3 Graph Pad |
A3 Drawing Board |
Drawing and Sketching Pencil Art Set |
Coloured Pencil Set |
A3 Light Box |