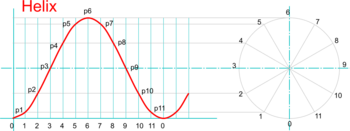
A Helix is the locus of a point travelling with constant linear velocity, axially along the outside of a cylinder as the cylinder rotates with constant angular velocity. The axial distance travelled by the point for each revolution of the cylinder is known as the pitch.
A helix is the curve used to produce a screw and is common in screwthreads and coil springs.
The elevation of this locus is a Sine Curve, which is also the curve used on a Displacement Diagram to generate Simple Harmonic Motion to a Cam Follower.
| Drawing a Helix
|
- Start by drawing a circle to represent the diameter of the generating cylinder and divide it into equal sectors (say,12)
- Project horizontal lines along from each intersection between the radial dividing lines and the circle circumference.
- Make the length of these lines equal to the pitch of the helix to be drawn (or a mulitple of it if several ‘turns’ are needed).
- Start at 0 then plot Point 1 where the projection line from position 1 on the circle intersects the first vertical dividing line of the pitch as shown.
- Continue for all other points then sketch a fair curve through them to create the helix (or use French Curves or a flexible strip for example)
|
|
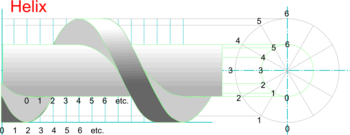
| Drawing Helical Screws and Springs
|
- Helical objects, such screwthreads and springs for example, are drawn in a similar way.
- Start by drawing two concentric circles: one equal to the outside diameter of the object and one equal to the inside diameter.
- Project horizontal lines from each circle as above and plot two helixes: one along the inner circle lines and one along those projected from the outer circle and sketch fair curves through these two to avoid confusion later.
- Choose a second starting point, furher along the pitch, and repeat to draw two more helixes as shown and sketch fair curves through them as before.
- Careful visualisation and selection of which parts of the helixes are in front and which are hidden will then enable a 3D screw-type form to be completed.
|
|
Note:
To draw an actual thread or spring its cross-section must be drawn at the starting point 0 and this used to determine the inner (or ‘core’) diameter, the pitch, and the number of helixes required.