Finding out about forces in a simple beam
From DT Online
Place a sheet of thin card between two blocks of wood to create a simple beam bridge. The distance between the supports is known as the Span. Note that the card can hardly support its own weight and soon bends or deflects if an extra load is added.
Activity:
- What can you do to the paper to enable it to support itself better? Think about Corrugated Card.
- Is it best to increase the length, width or depth of the card bridge? See Folded Paper Beam for ideas.
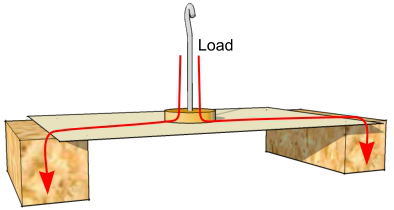
Bridges have to support two loads: their own weight and any loads they are required to carry. Their own weight is a fixed amount and is known as the Dead Load. The additional amount a bridge has to carry can vary continuously (e.g. as traffic passes over or as the wind blows) and it is known as the Live Load. Bridges and other structures also have to cope with the effects of wind, weather and the constant heating and cooling as a result of day and night temperature differences.
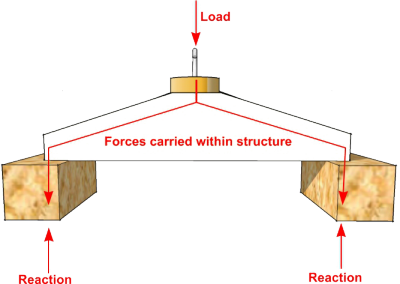
Bridges (and most other structures) deal with these loads by carrying them as forces through the structure until they come up against something firm enough to resist them - in the case of bridges, this is usually the solid earth.
When the forces reach the bridge supports, or Abutments, they are met with equal and opposite forces known as the Reactions - check on Newton's 3rd Law of Motion to learn why this must be so (i.e. ‘to every action there is always an equal and opposite reaction’).
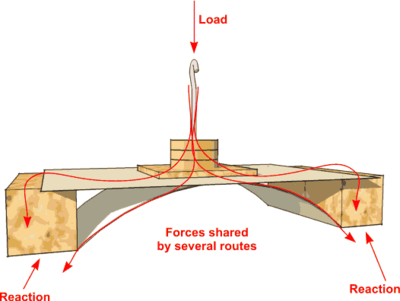
Bridge designers deal with these internal forces by either providing enough material for there to be several routes through, so the forces are shared, or by adding additional support in some way - e.g. by a supporting Arch. They also try to minimise the bridge self-weight by using open framed structures instead of solid beams.
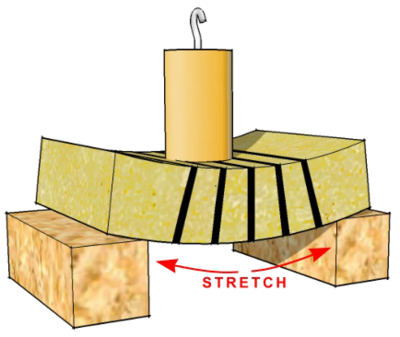
Designers must also make sure that each part of the structure is able to resist the forces generated within it. A simple beam will bend or deflect when loaded. Draw vertical lines on a simply supported sponge, or piece of rubber, to see that the top surface is squeezed together and the bottom surface is pulled apart when it is loaded.
Activity:
- If the top compresses and the bottom stretches, what do you think happens along the centre of the sponge? Does it squash a little, stretch a little or stay the same? See Neutral Axis to find out.
- See Beam Bridge Models and try out different designs.
- What would happen if a weight or load was dropped on to the beam instead of placing it carefully?