Displacement Diagram
From DT Online
Description
A Displacement Diagram is essentially a graph which plots the movement of a cam follower against time.
Since the cam's movement is usually constant then equal time intervals can be represented by equal distances along the horizontal axis and the resulting follower movement (or ‘displacement’) along the vertical axis.
During a single cam operated sequence, the follower may have periods of rest, or Dwell, when it neither rises nor falls. This would be represented by a horizontal line. It may be required to experience a Sudden Drop down to a lower position and this would be represented by a vertical line on the graph.
Features and Applications
The rise or fall of the follower may describe various types of motion as follows:
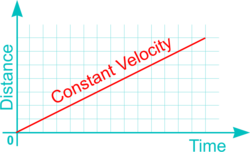
| Constant velocity (CV) | - | The follower simply rises or falls from one position to another at a constant speed (i.e. it travels the same distance during equal time intervals): it is represented by a straight line on the graph as shown. | |
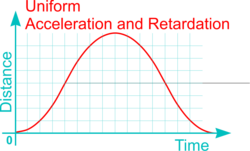
| Uniform Acceleration and Retardation (UAR) | - | The follower rises and falls as if a ball thrown in the air: this motion is represented by a parabola on the graph. | |
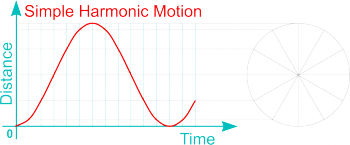
| Simple Harmonic Motion (SHM) | - | This is defined as the projection of a point on the diameter as it moves around a circle with uniform angular velocity. It is the motion of a pendulum or bouncing spring and provides a very smooth transition between rise and fall. This follower movement is approximated by an Eccentric Cam but can be more precisely plotted on the graph using a Sine Curve. | |
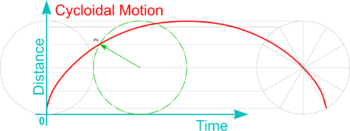
| Cycloidal Motion | - | This is the curve of fastest descent under gravity: it can be represented on the graph by drawing a cycloid (i.e. the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line without slippage) . |
The Displacement Diagram is in itself the profile of a Linear Cam and could simply be cut out and wrapped around a tube to form the profile of a Cylindrical Cam (the horizontal 'Time' axis of the Displacement Diagram is equal to the circumference and represents a single revolution).
In addition, to create a Radial Cam all vertical distances on the graph must be transferred to appropriately spaced radial lines on the cam profile. Periods of Dwell become concentric circles and a Sudden Drop is represented by a radial line - a Snail Cam can provide a common example of this.
|
Click top left to enlarge |
 |
 |
 |
 |
 |
| Engino "STEM Mechanics" Cams and Cranks Set |
Engino "STEM Mechanics" Levers and Linkages Set |
Fischertechnik 536622 - Mechanic & Static 2 |
Engino Mechanisms Set |
Engino Gears Set |