Exploring Sundials

Introduction

A Sundial of sorts can quite easily be made by pushing a pencil through the centre of a paper plate and placing it in a sunny position such that the pencil casts a shadow.

If the paper plate is divided into 24 equal segments (i.e. each 15 degrees) then this would work quite well at the North Pole, since the Sun appears to do a full 360⁰ rotation of the Earth every 24 hours (i.e. 360 ÷ 24 = 15). If placed anywhere other than the North Pole, however, it would soon become apparent that equal segments are not the answer if the pencil is vertical.

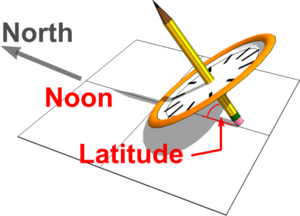
The rod or edge projecting the shadow (e.g. the pencil in this case), known as the Gnomon, must be arranged always to point North and be parallel to the Earth's axis for a Sundial to maintain good time throughout the year. In this orientation, the Sun can appear to be rotating around it as if it were placed at the North Pole (see Sundials and Gnomons).

The correct orientation can be achieved simply by tilting the paper plate and pencil until the pencil is lying at an angle equal to the Latitude of where the Sundial is to be positioned (e.g. approximately 51.5⁰ for London).

It can be imagined that a Sundial designed to sit at the North Pole would be identical to one placed at the centre of the Earth on the Equator, if that were possible, and so Sundial with equally spaced divisions as shown are known as Equatorial Sundials. These can be regarded as ‘master sundials’ from which designs for others may be generated.

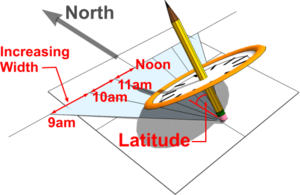
Horizontal Sundial

The tilted dial of an Equatorial Sundial is not always convenient and so consideration must be given to designing a Sundial with a horizontal dial. This is achieved by imagining the shadows cast to be projected on to a horizontal plate. Lines are drawn from where the Gnomon rests on the plate, along the lines of each shadow, to generate a series of hour lines on the horizontal dial.

As is the case with other Sundials, the Gnomon remains pointing North and at an angle equal to the Latitude of where the Sundial is to be positioned. Note that the angles between the hour lines increase as the Sun's shadow deviates away from Noon during both morning and afternoon. This gives rise to the familiar splayed lines on a modern Horizontal Sundial and as seen on the face of the Ancient Egyptian sundial discovered in the Valley of the Kings around 1500 BC.

The calculation of the angles for the hour lines requires some quite advanced Trigonometry as follows:

Horizontal dial shadow angle θ = Arctan (Sin Latitude(L) x Tan H)

Where:

θ = the hour angle (i.e. the deviation away from the North-facing Noon line);
L = the Latitude of the sundial location;
H = the number of hours either side of Noon x 15⁰.

The results will show that Horizontal Sundials work best at higher Latitudes rather than near the Equator.

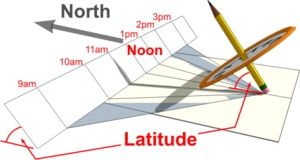
Vertical Sundial

As with a Horizontal Sundial the Gnomon remains pointing North and set at an angle to the horizontal equal to the Latitude of the Sundial location. The Gnomon therefore must be set at an angle to the 'dial' of 90⁰. minus Latitude.

Ideally, the 'dial' of a Vertical Sundial should be fixed to a South-facing wall or surface. In this situation the Gnomon is located in a plane at right angles to the 'dial' and will cast a vertical shadow at Noon. If placed on a wall which is not South-facing (e.g. S.E. or S.W.) then the Gnomon will need to be angled to the 'dial' such that the shadow cast at Noon remains vertical and is said to be Declined East or West as appropriate.

The calculation of the angles for the hour lines requires similar advanced Trigonometry as for Horizontal Sundials:

Vertical dial shadow angle θ = Arctan (Cos Latitude(L) x Tan H)

Where the variables are the same as given above for the Horizontal Sundial but note that it is the Cosine of Latitude which is used rather than the Sine.

The results will show that Vertical Sundials work well if nearer to the Equator than the North Pole.

Note: To check your Hour Lines, DT Online Design Tools are available HERE which calculate each hour line for any given Latitude which is input and optionally print-out a Template of the resulting 'Dial Plate'.

Polar Sundial

If a strip,of material is placed across the end of a Horizontal Sundial such that the Sun's shadows are able to project on to it, and tilted at the Latitude angle, it will be seen that the shadows generate parallel lines on the tilted plate. As the distance to the 6am and 6pm hour lines approach infinity (i.e. when the Sun's rays are parallel to the 'dial plate'), the time that can be indicated by the dial is limited to the practical width of the 'dial plate' (or the curve of the 'dial plate' in designs adopting this solution).

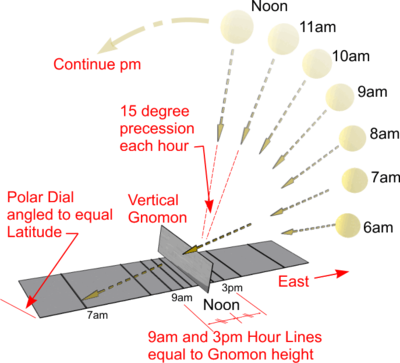
These are known as Polar Sundials: the 'dial plate' is fixed at an angle parallel with the Earth's axis; the Gnomon is parallel to the 'dial plate'; and the hour lines are parallel to each other along the length of the 'dial plate'. Typically the Gnomon is formed by the edge of a rectangular plate fixed across the centre of the 'dial plate' at the Noon position.

The distance between the parallel hour lines is determined only by the height of the Gnomon and is not affected by Latitude.

The Polar Sundial is universal and can be used at any Latitude.The 'dial plate' is oriented East-West and the Gnomon points North as with other Sundials. The Sun appears to orbit Westward from Noon at a rate of 15⁰ each hour and so will cast shadows from the Gnomon at an angle of 45⁰ to it at 3pm. This will result in the hour lines for both 9am and 3pm being at a distance from the Gnomon which is equal to its height.

The distance of other hour lines from the Gnomon may be calculated using Trigonometry as follows:

Distance X = Gnomon Height(G) x Tan H

Where:

X = the distance of an hour line from the Noon line (i.e. the Gnomon position).
G = the height of the Gnomon above the 'dial plate';
H = the number of hours either side of Noon x 15⁰.

The Polar Sundial is similar in many ways to the Merkhet or Instrument of Knowing used by Ancient Egyptians to align their Pyramids.

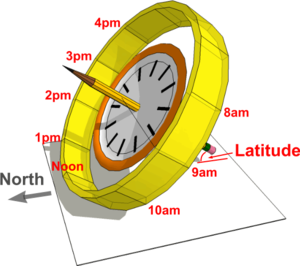
Armillary (or Ring) Sundials

As with other Sundials, the Gnomon of an Armillary Sundial points North and is set at an angle to the horizontal equal to the Latitude.

They can be considered as a type of Equatorial Sundial in that instead of a disc being fixed at right angles to the Gnomon, it is replaced by a ring which would be concenric with it.

The ring is known as the Equatorial Ring and the hour lines are spaced equally around it at 15⁰. intervals.

Developments of this design include Armillary Spheres in which additional rings are added. A second ring rotated 90⁰ around from the Equatorial Ring for example, such that the Gnomon lies along its diameter, can be graduated with degrees of Latitude and the Gnomon made adjustable around it to accommodate different locations.