Young's Modulus: Difference between revisions
From DT Online
mNo edit summary |
mNo edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 3: | Line 3: | ||
The '''[[Stress]]''' divided by the '''[[Strain]]''' during this '''Elastic Stage''' is a measure of the [http://en.wikipedia.org/wiki/Stiffness '''stiffness'''] of a material and is known as its [ | The '''[[Stress]]''' divided by the '''[[Strain]]''' during this '''Elastic Stage''' is a measure of the [http://en.wikipedia.org/wiki/Stiffness '''stiffness'''] of a material and is known as its [http://en.wikipedia.org/wiki/Young's_modulus '''Young's Modulus'''] or [http://en.wikipedia.org/wiki/Elastic_modulus '''Modulus of Elasticity'''] | ||
| Line 16: | Line 16: | ||
The '''Young's Modulus''' is a fundamental property of the material and is unchanged by '''[[Heat Treatment]]''' processes such as '''[[Heat Treatment|Annealing]]''' or '''[[ | The '''Young's Modulus''' is a fundamental property of the material and is unchanged by '''[[Heat Treatment]]''' processes such as '''[[Heat Treatment|Annealing]]''' or '''[[Crystalline_Structures#Work_Hardening|Work Hardening]]''' - you simply change degrees of '''[[Elasticity]]''' and '''[[Plasticity]]'''. The shape of the '''Stress/Strain Curve''' therefore changes but the area under it remains the same because the work done to fracture is constant. | ||
[[Category:Terminology]] | [[Category:Terminology]] | ||
Latest revision as of 11:47, 21 March 2017
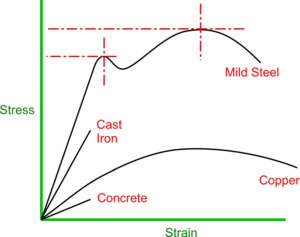
As material samples are stretched, initially, the Stress is directly proportional to the Strain - producing the straight line as shown on the graph. The material is behaving in much the same way as a spring would under tension and, if the force is removed, the material returns to its original length. The material is obeying Hooke's Law and this phase is known as the Elastic Stage.
The Stress divided by the Strain during this Elastic Stage is a measure of the stiffness of a material and is known as its Young's Modulus or Modulus of Elasticity
If a force is continued to be applied beyond this phase, the material reaches a point at which it stays permanently stretched. This is the Yield Point or Elastic Limit and beyond this, during its Plastic Stage, the material will continue to remain permanently deformed until eventually it breaks.
Much can be determined about a material from its Stress/Strain Curve - for example, Ductile materials will exhibit an extended Plastic Stage whereas Brittle materials would have little or none at all. In short:
- a stiffer material will exhibit a steeper slope
- a brittle material will lack a plastic region
- a stronger material will show a higher U.T.S.
The Young's Modulus is a fundamental property of the material and is unchanged by Heat Treatment processes such as Annealing or Work Hardening - you simply change degrees of Elasticity and Plasticity. The shape of the Stress/Strain Curve therefore changes but the area under it remains the same because the work done to fracture is constant.