Intersecting Chords: Difference between revisions
From DT Online
m (Removed a category) |
mNo edit summary |
||
| Line 20: | Line 20: | ||
* but, for small deflections, Δ<sup>2</sup> will be negligible | * but, for small deflections, Δ<sup>2</sup> will be negligible | ||
* so '''Bending Radius ''(R)'' = cd<sup>2</sup> ÷ (8 x Δ)''' | * so '''Bending Radius ''(R)'' = cd<sup>2</sup> ÷ (8 x Δ)''' | ||
''(see | ''(see [https://www.amazon.co.uk/gp/product/0306812835/ref=as_li_qf_sp_asin_il_tl?ie=UTF8&camp=1634&creative=6738&creativeASIN=0306812835&linkCode=as2&tag=dton06-21 ''''Structures: Or Why Things Don't Fall Down' by J.E.Gordon'''])'' </span> | ||
|[[File:BeamChordsTheorem.png|400px|right]] | |[[File:BeamChordsTheorem.png|400px|right]] | ||
|} | |} | ||
Revision as of 10:03, 14 November 2016
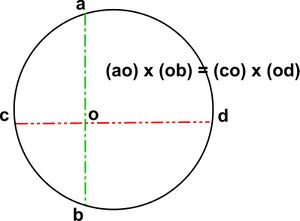
This theorem relates to a characteristic of a cyclic quadlitateral, the diagonals of which are two intersecting chords of the circumscribing circle.
The Intersecting Chords Theorem states that the relationship (ao x ob = co x od) is true for any two intersecting chords, whether or not one of them is a diameter.
| Measuring Beam Deflections |
The theorem can be useful when measuring the radius of bending of a deflected beam if one of the chords is taken to be the length of the beam e.g.
Bending Radius (R) can be calculated as follows:
(see 'Structures: Or Why Things Don't Fall Down' by J.E.Gordon) |