Intersecting Chords: Difference between revisions
From DT Online
Improved presentation |
mNo edit summary |
||
| Line 19: | Line 19: | ||
* (2R-Δ) x Δ = ½cd x ½cd | * (2R-Δ) x Δ = ½cd x ½cd | ||
* but, for small deflections, Δ<sup>2</sup> will be negligible | * but, for small deflections, Δ<sup>2</sup> will be negligible | ||
* so R = cd<sup>2</sup> ÷ 8 x Δ | * so '''Bending Radius ''(R)'' = cd<sup>2</sup> ÷ (8 x Δ)''' | ||
''(see ‘Structures’ by [http://en.wikipedia.org/wiki/J.E._Gordon J.E.Gordon] ISBN 0 14 02.1961 7)'' </span> | ''(see ‘Structures’ by [http://en.wikipedia.org/wiki/J.E._Gordon J.E.Gordon] ISBN 0 14 02.1961 7)'' </span> | ||
|[[File:DeflectedBeamChords.jpg|400px|right]] | |[[File:DeflectedBeamChords.jpg|400px|right]] | ||
Revision as of 08:34, 27 February 2015
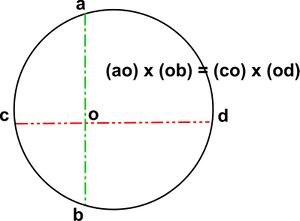
This theorem relates to a characteristic of a cyclic quadlitateral, the diagonals of which are two intersecting chords of the circumscribing circle.
The Intersecting Chords Theorem states that the relationship (ao x ob = co x od) is true for any two intersecting chords, whether or not one of them is a diameter.
| Measuring Beam Deflections |
The theorem can be useful when measuring the radius of bending of a deflected beam if one of the chords is taken to be the length of the beam e.g.
Bending Radius (R) can be calculated as follows:
(see ‘Structures’ by J.E.Gordon ISBN 0 14 02.1961 7) |