Intersecting Chords

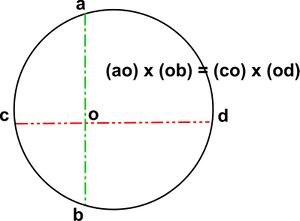
This theorem relates to a characteristic of a cyclic quadlitateral, the diagonals of which are two intersecting chords of the circumscribing circle.

The Intersecting Chords Theorem states that the relationship (ao x ob = co x od) is true for any two intersecting chords, whether or not one of them is a diameter.

Measuring Beam Deflections

The theorem can be useful when measuring the radius of bending of a deflected beam if one of the chords is taken to be the length of the beam e.g. set up a strip of material as a simple beam note the distance between supports (cd) apply a central load to make it bend - or ‘deflect’(Δ) - therefore co = od = ½cd measure the deflection (ob) Bending Radius (R) can be calculated as follows: ao x ob = co x od (2R-Δ) x Δ = ½cd x ½cd but, for small deflections, Δ2 will be negligible so R = cd2 ÷ 8 x Δ (see ‘Structures’ by J.E.Gordon ISBN 0 14 02.1961 7)

File:DeflectedBeamChords.jpg