Exploring Sundials

Introduction

A Sundial of sorts can quite easily be made by pushing a pencil through the centre of a paper plate and placing it in a sunny position such that the pencil casts a shadow.

If the paper plate is divided into 24 equal segments (i.e. each 15 degrees) then this would work quite well at the North Pole, since the Sun appears to do a full 360⁰ rotation of the Earth every 24 hours (i.e. 360 ÷ 24 = 15). If placed anywhere other than the North Pole, however, it would soon become apparent that equal segments are not the answer if the pencil is vertical.

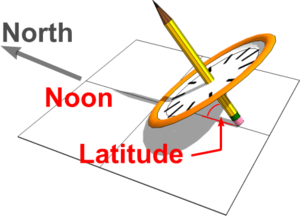
The rod or edge projecting the shadow (e.g. the pencil in this case), known as the Gnomon, must be arranged always to point North and be parallel to the Earth's axis for a Sundial to maintain good time throughout the year. In this orientation, the Sun can appear to be rotating around it as if it were placed at the North Pole.

The correct orientation can be achieved simply by tilting the paper plate and pencil until the pencil is lying at an angle equal to the Latitude of where the Sundial is to be positioned (e.g. approximately 51.5⁰ for London).

It can be imagined that a Sundial designed to sit at the North Pole would be identical to one placed at the centre of the Earth on the Equator, if that were possible, and so Sundials with equally spaced divisions as shown are known as Equatorial Sundials. These can be regarded as ‘master sundials’ from which designs for others may be generated.

Horizontal Sundial

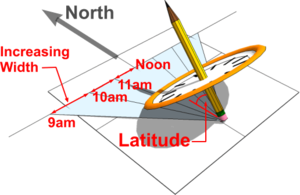
The tilted dial of an Equatorial Sundial is not always convenient and so consideration must be given to designing a Sundial with a horizontal dial. This is achieved by imagining the shadows cast to be projected on to a horizontal plate. Lines are drawn from where the Gnomon rests on the plate, along the lines of each shadow, to generate a series of hour lines on the horizontal dial.

As is the case with other Sundials, the Gnomon remains pointing North and at an angle equal to the Latitude of where the Sundial is to be positioned. Note that the angles between the hour lines increase as the Sun's shadow deviates away from Noon during both morning and afternoon. This gives rise to the familiar splayed lines on a modern Horizontal Sundial and as first discovered on the face of the Ancient Egyptian sundial discovered in the Valley of the Kings around 1500 BC.

The calculation of the angles for the hour lines requires some quite advanced Trigonometry as follows: Horizontal dial shadow angle θ = Arctan (Sin Latitude(L) x Tan H)

Where: